原文:Deep Learning with Swift for TensorFlow
协议:CC BY-NC-SA 4.0
毫无疑问,我们从事的是铸造神灵的工作。 1
——帕梅拉·麦科达克
如今,除了量子计算(Preskill,2018)和区块链(Nakamoto,2008),人工智能(AI)是计算机科学最迷人的领域之一。自 2000 年代中期以来,工业界的大肆宣传导致了对人工智能初创公司的大量投资。全球领先的科技公司,如苹果、谷歌、亚马逊、脸书和微软,仅举几例,正在迅速收购世界各地有才华的人工智能初创公司,以加速人工智能研究,并反过来改进自己的产品。
考虑像 Apple Watch 这样的便携式设备。它使用机器智能来分析你的实时运动感觉数据,以跟踪你的脚步、站立时间、游泳次数、睡眠时间等。它还可以根据手腕皮肤下暂时的血液颜色变化计算您的心率,提醒您心跳不规则,执行心电图(ECG),测量运动期间血液中的耗氧量(VO max)等等。另一方面,iPhone 和 iPad 等设备使用来自相机传感器的激光雷达信息来即时创建周围的深度图。这些信息然后与机器智能相结合,以提供计算摄影功能,如强度可调的散景效果,沉浸式增强现实(AR)功能,如 AR 对象上周围的反射和照明,人类进入场景时的对象遮挡,等等。像 Siri 这样的个人语音助理可以理解你的语音,让你完成各种任务,例如控制你的家庭配件,在 HomePod 上播放音乐,给别人打电话和发短信,等等。机器智能技术因快速图形处理单元(GPU)而成为可能。如今,便携式设备上的 GPU 足够快,可以处理用户的数据,而不必将其发送到云服务器。这种方法有助于保持用户数据的私密性,从而防止不良暴露和使用(Sharma 和 Bhalley,2016 年)。事实上,上面提到的所有功能都可以通过设备上的机器智能来实现。
你可能会惊讶,人工智能并不是一项新技术。它实际上可以追溯到 20 世纪 40 年代,人们根本不认为它有用和酷。它有许多起伏。人工智能技术的普及主要有三次。它在这些时代有不同的名字,现在我们普遍认为它是深度学习。20 世纪 40-60 年代间,艾被称为“控制论”;大约在 20 世纪 80-90 年代,它被称为“连接主义”;从 2006 年开始,我们将人工智能称为“深度学习”。
在过去的某个时候,也有一种误解,许多研究人员认为,如果宇宙中所有事物工作方式的所有规则都被编程到计算机中,那么它就会自动变得智能。但这一想法受到了人工智能现状的强烈挑战,因为我们现在知道有更简单的方法来让机器模仿类似人类的智能。
在人工智能研究的早期,数据很少。计算机器也很慢。这些是淹没人工智能系统流行的主要因素之一。但现在我们有了互联网,地球上很大一部分人相互交流,迅速产生海量数据,这些数据存储在各自公司的服务器上。(刘冰等人,2009 年)找到了一种以更快速度运行深度学习算法的方法。大数据集和高性能计算(HPC)的结合使研究人员快速推进了最先进的深度学习算法。这本书的重点是从简单的概念开始向你介绍这些先进的算法。
在这一章中,我们将介绍机器学习的基本概念,这些概念对其继任者深度学习领域仍然有效。第章 2 重点讲述清楚理解深度学习算法所需的数学。因为深度学习是一门经验学科,如果我们自己不能编程,那么只理解深度学习算法的数学方程是没有用的。此外,计算机是通过执行数值计算来测试数学定理的(图灵,1936)。第三章介绍了一种强大的、经过编译的、快速的深度学习编程语言,称为 Swift for TensorFlow,它扩展了苹果的 Swift 语言(已经能够进行差异化编程),以包括深度学习特有的 TensorFlow 库功能。TensorFlow 是一个深度学习专用的库,值得整个章节 4 专门介绍它。然后我们在第五章中深入研究神经网络的基础知识。最后我们会在第六章编程一些高级的计算机视觉算法。
但让我们首先区分人工智能、机器学习和深度学习这三个术语,因为它们有时会互换使用。人工智能,也称为机器智能,代表了一套可用于使机器智能化的算法。人工智能系统通常包含硬编码的规则,程序遵循这些规则来从数据中获取一些意义(Russell & Norvig,2002),例如,使用硬编码的英语语法规则在句子中找到名词,使用 if 和 else 条件防止机器人掉入陷阱,等等。如今这些系统被认为是弱智能的。另一个术语是机器学习(ML),与人工智能算法不同的是,它使用数据来从中获得洞察力(Bishop,2006),例如,使用 k-最近邻等非参数算法对图像进行分类,使用决策树方法对文本进行分类,等等。ML 使用数据来学习,并且也已知表现弱于深度学习。最后,目前最先进的 AI 是深度学习。深度学习(DL)也使用数据进行学习,但采用分层方式(LeCun 等人,2015 年),从大脑中获取灵感。DL 算法可以很容易地学习非常复杂的数据集的映射,而不会损害准确性,但它们的表现反而比机器学习算法更好。如果你画一个维恩图,如图 1-1 所示,你会看到深度学习是机器学习的一个子集,而人工智能领域是这两个领域的超集。
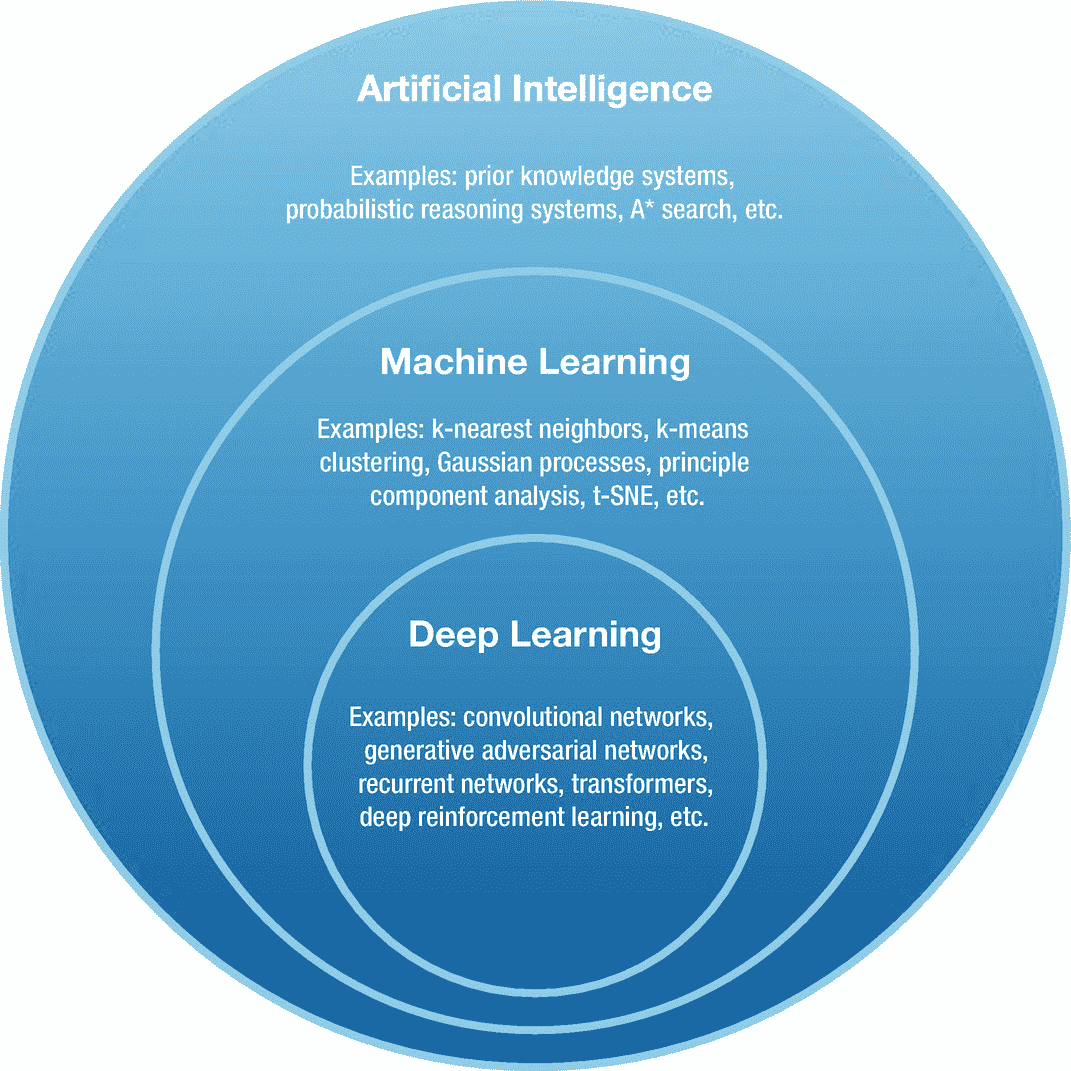
图 1-1
代表人工智能、机器学习和深度学习算法之间重叠(未精确缩放)的维恩图。每套给出了属于那个领域的算法的几个例子。
现在,我们可以从简单的机器学习概念开始深度学习之旅。
机器学习算法通过从数据中学习自身来学习执行某些任务,同时提高其性能。机器学习的广泛接受的定义(Mitchell 等人,1997)如下:“如果计算机程序在任务 T 的性能(由 P 测量)随着经验 E 而提高,则称该计算机程序从关于某类任务 T 和性能测量 P 的经验 E 中学习。”其思想是编写一个计算机程序,该计算机程序可以通过一些性能测量来更新其状态,以通过体验可用数据以良好的性能执行期望的任务。让这个程序学习不需要人工干预。
基于这个定义,有三个基本概念可以帮助我们让机器学习,即经验、任务和性能测量。本节将讨论这些想法。在 1.4 节中,我们将看到这些思想是如何用数学方法表达的,这样就可以编写一个学习型计算机程序。在 1.4 节之后,你会意识到这个简单的定义形成了机器如何学习的基础,并且书中讨论的每个机器学习范例都可以用这个定义来隐含地表达。
在我们进一步进行之前,澄清机器学习算法由各种基本组件组成是很重要的。它的学习部分被称为模型,它只是一个数学函数。现在让我们继续理解这些基本思想。
经验是模型为了学习执行任务而进行的多次观察。这些观察结果是来自可用数据集的样本。在学习过程中,总是需要一个模型来观察数据。
数据可以是各种形式,例如图像、视频、音频、文本、触觉等。每个样本,也被称为样本,从数据上可以用其特征来表示。例如,图像样本的特征是其像素,其中每个像素由红色、绿色和蓝色值组成。所有这些颜色的不同亮度值一起代表电磁辐射光谱的可见范围(我们的眼睛可以感知)中的单一颜色。
除了特征,每个样本有时还可能包含一个对应的标签向量,也称为目标向量,代表样本所属的类别。例如,鱼图像样本可能具有代表鱼的相应标签向量。标签通常用 one-hot 编码(也称为 - k 编码的 1- ,其中 k 是类的数量)来表示,这是一种表示,其中整个向量中只有单个索引的值为 1,其他所有索引都设置为 0。假设每个指数代表某一类,值为 1 的指数假设代表样本所属的类。例如,假设[1 0 0]向量代表一只狗,而[0 1 0]和[0 0 1]向量分别代表一条鱼和一只鸟。这意味着鸟类的所有图像样本都具有相应的标签向量[0 0 1],同样,狗和鱼的图像样本也将具有它们自己的标签。
我们之前列出的样本特征是原始特征,也就是说,这些特征不是由人类精心挑选的。有时,在机器学习中,特征选择对模型的性能起着重要的作用。例如,对于像人脸识别这样的任务,高分辨率图像比低分辨率图像处理起来要慢。因为深度学习可以直接在原始数据上工作,性能非常好,所以我们不会特别讨论特征选择。但是,当代码清单中需要以正确的格式获取数据时,我们将介绍一些预处理技术。我们建议感兴趣的读者参考(泽奥多里德斯和库特鲁姆巴斯,2009 年)教科书来了解特征选择。
在深度学习中,我们可能需要对数据进行预处理。预处理是应用于原始样本的一系列函数,将它们转换成所需的特定形式。这种期望的形式通常是基于模型的设计和手头的任务来决定的。例如,以 16 KHz 采样的原始音频波形每秒有 16,384 个样本被表示为向量。即使对于一个短的音频记录,比如说 5 秒,这个向量的维数也会变得非常大,也就是说,一个 81,920 元素长的向量!我们的模型需要更长的时间来处理。这就是预处理变得有用的地方。然后,我们可以使用快速傅立叶变换(Heideman 等人,1985)函数对每个原始音频波形样本进行预处理,以将其转换为频谱图表示。现在,该图像的处理速度比之前冗长的原始音频波形快得多。有不同的方法来预处理数据,选择取决于模型设计和手头的任务。我们将在本书中介绍不同类型数据的一些预处理步骤,并不详尽,只要有需要。
任务是模型处理样本特征以返回样本的正确标签的动作。设计机器学习模型主要有两个任务,即回归和分类。还有更多有趣的任务,我们将在后面的章节中介绍和编程,它们只是这两个基本任务的扩展。
例如,对于一幅鱼的图像,模型应该返回[0 1 0]向量。因为这里图像被映射到它的标签,这个任务通常被称为图像分类。这是分类任务的一个简单示例。
回归任务的一个很好的例子是对象检测。我们可能想要在图像中检测一个物体的位置,比如球。这里,特征是图像像素,标签是图像中对象的坐标。这些坐标表示对象的边界框,即对象在给定图像中出现的位置。这里,我们的目标是训练一个模型,该模型将图像特征作为输入,并预测对象的正确结合框坐标。因为预测输出是实值的,所以对象检测被认为是回归任务。
一旦我们设计了一个执行任务的模型,下一步就是让它学习并评估它在给定任务上的表现。为了评估,使用某种形式的性能测量(或度量)。性能度量可以采用各种形式,如准确性、F1 分数、精确度和召回率等,来描述模型执行任务的好坏。请注意,在训练和测试阶段,应该使用相同的性能指标来评估模型。
根据经验,只要有可能,就必须尝试选择一个单一数字的性能指标。在我们之前的图像分类示例中,可以很容易地使用准确度作为性能度量。精度定义为被模型正确分类的图像(或其他样本)总数的一部分。如下所示,也可以使用多数字性能指标,但这使得从一组训练模型中确定哪个模型表现最佳变得更加困难。
让我们考虑两个图像分类器 C 1 和 C 2 ,它们的任务是预测图像中是否包含汽车。如表 1-1 所示,如果分类器 C 1 的精度为 0.92,分类器 C 2 的精度为 0.99,那么很明显 C 2 的性能优于 C 1 。
表 1-1
分类器 C 1 和 C 2 在图像识别任务中的准确度。
|分类者
|
准确
|
| --- | --- |
| C 1 | 92% |
| C 2 | 99% |
现在让我们考虑这两个分类器的精确度和召回率,这是一个两个数字的评估度量。精度和召回被定义为分类器分别正确标记为汽车的测试或验证集中所有和汽车图像的的分数。对于我们的任意分类器,这些度量值如表 1-2 所示。
表 1-2
分类器 C 1 和 C 2 在图像识别任务中的精度和召回率。
|分类者
|
精确
|
回忆
|
| --- | --- | --- |
| C 1 | 98% | 95% |
| C 2 | 95% | 90% |
现在似乎还不清楚哪种型号的性能更优越。相反,我们可以将精确度和召回率转化为一个单一的数字指标。有多种方法可以实现这一点,如均值或 F 1 得分。在这里,我们将找到它的 F 1 分数。 F
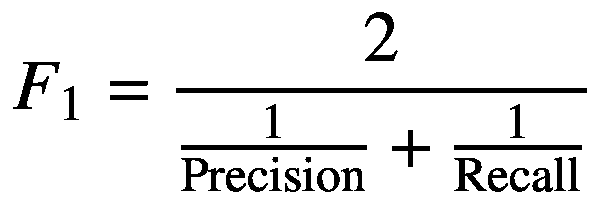
(1.1)
表 1-3 通过将每个分类器的精度和召回值放入等式 1.1 来显示每个分类器的 F 1 分数。
从表 1-3 中,简单看一下 F 1 的分数,我们很容易得出分类器 C 2 比 C 1 表现更好的结论。在实践中,使用一个单一的评估指标对于确定训练模型的优越性非常有帮助,并且可以加速您的研究或部署过程。
表 1-3
分类器 C 1 和 C 2 在一个图像识别任务上的精度、召回率和 F 1 得分。
|分类者
|
精确
|
回忆
|
F1 分数
|
| --- | --- | --- | --- |
| C 1 | 98% | 85% | 91% |
| C 2 | 95% | 90% | 92.4% |
已经讨论了机器学习的基本思想,我们现在将把我们的焦点转向不同的机器学习范例。
机器学习通常根据数据集经验的种类分为四类,允许的模型如下:监督学习(SL)、非监督学习(UL)、半监督学习(SSL)和强化学习(RL)。我们简要讨论这些机器学习范例中的每一个。
在训练期间,当一个模型利用带标签的数据样本来学习执行任务时,这种类型的机器学习被称为监督学习。它被称为“有监督的”,因为属于数据集的每个样本都有相应的标签。在监督学习中,在训练期间,机器学习模型的目标是从样本映射到它们相应的目标。在推断过程中,监督模型必须预测任何给定样本的正确标签,包括训练过程中未看到的样本。
我们之前已经讨论了图像分类任务的概念,这是 SL 的一个例子。例如,你可以通过在苹果的照片应用程序中输入照片中出现的对象的类别来搜索照片。另一个有趣的 SL 任务是自动语音识别(ASR ),其中一系列音频波形被模型转录成表示音频记录中所说单词的文本序列。例如,Siri、Google Assistant、Cortana 和其他便携式设备上的个人语音助手都使用语音识别来将你所说的话转换成文本。在撰写本文时,SL 是生产中最成功和最广泛使用的机器学习。
无监督学习是一种机器学习,模型只允许观察样本特征,不允许观察标签。UL 通常旨在学习模型隐藏特征中数据集的一些有用表示。这个学习到的表示可以在以后使用这个模型执行任何期望的任务。在撰写本文时,深度学习社区对 UL 非常感兴趣。
例如,UL 可用于降低高维数据样本的维度,正如我们之前所讨论的,这有助于通过模型更快地处理数据样本。另一个例子是密度估计,目标是估计数据集的概率密度。在密度估计之后,模型可以产生与属于它被训练的数据集的样本相似的样本。正如我们将在后面看到的,UL 算法可以用来完成各种有趣的任务。
值得注意的是,UL 被称为“无监督的”,因为数据集中不存在标注,但我们仍然需要将标注与预测一起输入损失函数(这是第 1.3 节中讨论的最大似然估计的基本要求)以训练模型。在这种情况下,我们自己为样本假定一些适当的标签。例如,在生成式对抗性网络中(Goodfellow 等人,2014 年),从生成器生成的数据点的标签被赋予假标签(或 0),而从数据集采样的数据点被赋予真实标签(或 1)。另一个例子是自编码器(Vincent 等人,2008),其中标签是相应的样本图像本身。
半监督学习关注的是在训练期间,从一小组标记样本中训练一个模型,并预测(使用当前半训练模型)未标记样本为伪目标(也称为软目标)。从训练过程中经历的数据类型的角度来看,SSL 介于监督和非监督学习之间,因为它同时观察标记和未标记的样本。当我们有一个大的数据集,只包含少量的标记样本(因为它们很费力,因此获取起来很昂贵)和大量的未标记样本时,SSL 特别有用。有趣的是,用于训练该模型的 SSL 技术可以大大提高其性能。
我们在书中没有涉及半监督学习。对于半监督学习的严格理解,我们请感兴趣的读者参考(Chapelle 等人,2006)教科书。
强化学习是基于代理人与环境交互所获得的奖励,通过多次试验(称为情节)使其累积奖励(加权平均奖励序列,也称为回报)最大化,以实现其目标。RL 是一种机器学习的范式,涉及一系列决策过程。
代理通过采取一些行动来作用于世界,比如说它向前移动。在此之后,环境的状态得到更新,并且环境将奖励返回(或给予)给代理。根据行为科学的观点,奖励或者是积极的或者是消极的,并且可以分别被认为是世界对主体的好的或者坏的反应。我们更感兴趣的是回报,而不是当前的阶梯奖励,因为代理的目标是在每集的过程中最大化回报。在这里,一个情节是一个主体和它的环境之间从开始到结束的一系列相互作用。一集的例子如下:代理人的游戏,其中当满足某个条件时游戏结束,代理人试图在恶劣的环境条件下生存,直到由于某种事故而死亡。参见图 1-2 了解代理与其环境之间相互作用的示意图。
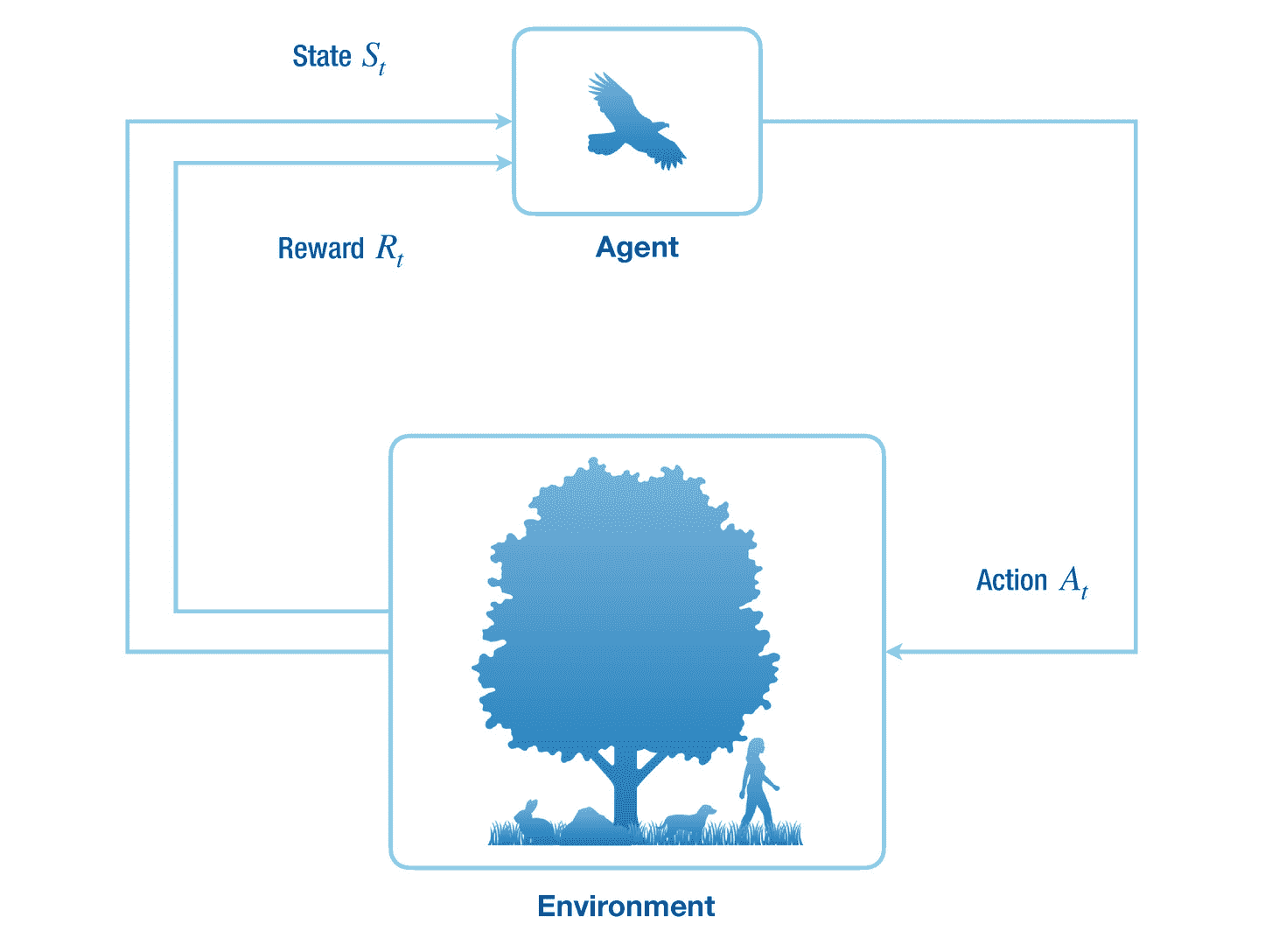
图 1-2
强化学习代理和环境之间的相互作用。
代理感知环境 S t -1 的先前状态,并对其状态 S t 改变的环境采取动作 A t ,并将其返回给代理。代理还从描述代理的当前状态有多好的环境接收标量奖励 R t 。虽然当代理动作时环境的状态改变,但它也可能自己改变。在多智能体强化学习中,也可能有其他智能体使自己的收益最大化。
强化学习是一个非常有趣的机器学习领域,在撰写本文时正在积极研究。它也被认为更接近于人类(或其他哺乳动物)通过进行行为修正来学习的方式,即在奖励的基础上强化一个动作。最近的一项工作(Minh et al .,2015)表明,一种称为深度强化学习的深度学习和强化学习的组合甚至可以超越人类级别的游戏能力。
不幸的是,我们在书中没有讨论强化学习。感兴趣的读者可以参考(萨顿和巴尔托,2018)教科书,了解该领域的基本知识。对于深度强化学习的进展,我们建议的作品(Mnih 等人,2015;舒尔曼等人,2017)。
现在让我们看看最大似然估计的基本思想,它有助于构建机器学习算法。
这里描述的设置在整个机器学习文献中都是假设的。在此设置的约束下,模型的参数被估计。解决参数估计问题有两种基本方法,即最大似然估计和贝叶斯推断。我们将关注最大似然估计,因为这是我们在整本书中用来训练神经网络的。建议对贝叶斯推理感兴趣的读者阅读(Bishop,1995)教材的第二章。关于最大似然函数起源的详细注释,请参考(Akaike,1973)。
为了解决一个机器学习问题,我们需要一个包含一组 N 个数据点(或样本)的数据集?,也就是? 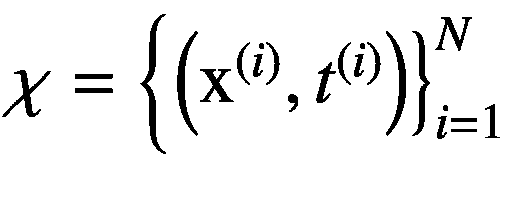 。假设每个数据点都是相同的,并且独立于联合数据生成分布Pd(x, t )进行采样,这是一个概率密度函数(PDF),意味着数据样本 x 和相应的目标 t 是连续的随机变量。注意,目标随机变量 t 的分布实际上取决于模型执行的任务,即目标的分布对于回归和分类任务分别是连续的和离散的。我们也将Pd(x, t )称为数据概率密度函数(或数据 PDF)。我们只能访问从数据 PDF 中采样的数据集?,而不能访问分布本身。因此,我们不能访问比我们可用的更多的数据点。
。假设每个数据点都是相同的,并且独立于联合数据生成分布Pd(x, t )进行采样,这是一个概率密度函数(PDF),意味着数据样本 x 和相应的目标 t 是连续的随机变量。注意,目标随机变量 t 的分布实际上取决于模型执行的任务,即目标的分布对于回归和分类任务分别是连续的和离散的。我们也将Pd(x, t )称为数据概率密度函数(或数据 PDF)。我们只能访问从数据 PDF 中采样的数据集?,而不能访问分布本身。因此,我们不能访问比我们可用的更多的数据点。
因为数据集?是从数据 PDF 中采样的,所以它以统计方式描述了数据 PDF 本身。我们在参数化机器学习中的目标是通过估计我们自己选择的参数化概率密度函数Pm(x, y | θ )(或者简单地说Pm(x, y )的参数来近似数据 PDF 的映射这里, θ 代表参数,随机变量 x 和 y 是数据样本和相应的预测值给定 x 作为输入。我们实际上将通过使用最大似然函数更新参数值来最小化预测变量 y 和目标变量 t 之间的距离,也称为损失或误差。
模型和数据 pdf 是完全不同的分布,因此它们的样本在统计上也是不同的。但是我们希望来自模型 PDF 的预测 y 类似于来自给定数据样本 x 的数据 PDF 的相应目标 t 。如前所述,我们无法访问数据 PDF 的参数,因此我们不能简单地将其参数值复制到模型函数的参数值中。但是我们确实有数据集 ?? 供我们使用,我们可以利用它来近似数据 PDF,因为这是它的统计描述。
现在我们将描述最大似然估计来用我们的参数化模型 PDF 近似数据 PDF。因为 ?? 中的数据点是独立且同分布的,它们的联合概率由下式给出
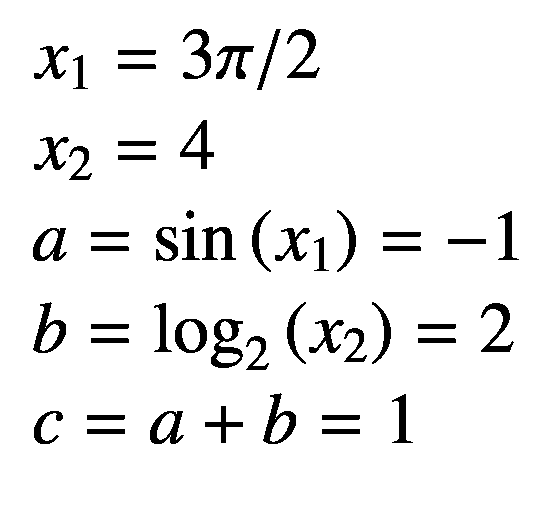
(1.2)
这里,pm(?|θ)是条件模型 PDF,读作“给定参数的数据集的联合概率”函数?( θ |?)是给定固定和有限数据集?.的参数 θ 的似然函数您也可以将此函数解释为“可能是对数据集?进行采样的数据 PDF 的良好近似”为了减少混乱,我们将隐含地假设模型和对数似然函数中的参数条件。我们将使用贝叶斯定理将联合数据概率分布转换为我们关心的条件分布。
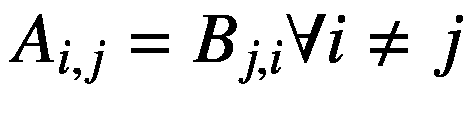
(1.3)
通过最大化似然函数来近似数据 PDF,这需要更新模型 PDF 的参数值。更具体地说,如 1.4 节中简要描述的和 5.1 节中详细描述的,参数是用迭代法更新的。在数值上,先取似然的负对数,然后最小化,这样更方便。这相当于最大化似然函数。
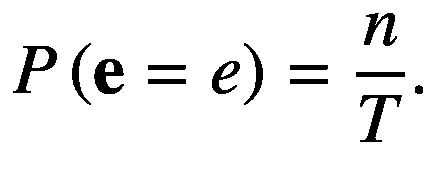
(1.4)
对数函数在这里起着非常重要的作用。它将乘积转化为总和,这有助于稳定数值计算。这是因为接近零的值的乘积是小得多的值,由于计算设备的有限精度表示能力,这些值可能被舍入。这也是机器学习频繁使用对数函数的原因。
负对数似然函数可被视为由 L 表示的损失或误差函数。).我们的目标是通过更新其参数值来最小化损失函数,使得我们的参数化模型 PDF 使用来自数据 PDF 的可用固定和有限数据样本来近似数据 PDF。请注意,该等式中的第二项对模型 PDF 的参数估计没有贡献,因为它不依赖于模型的参数,并且只是一个负的附加项,可以忽略该附加项以最大化似然函数。损失函数现在可以简单地用下面的等式来描述:
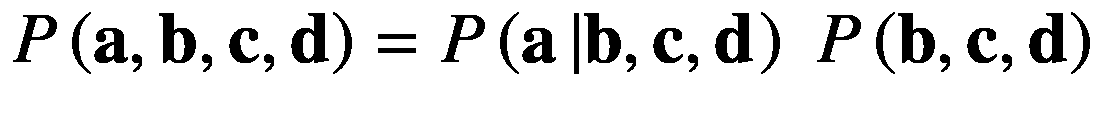
(1.5)
最小化损失函数相当于最小化负对数似然函数,负对数似然函数可以进一步被认为是最大化对数似然函数,因此术语最大似然估计。这里,我们的模型 PDF 表示给定数据样本的目标的条件分布Pm(t|x)。我们将在后面看到,神经网络是模拟这种条件分布的框架。并且也基于目标随机变量的分布,使用该方程产生不同的损失函数。
作为旁注,假设来说,如果似然函数完美地近似数据 PDF,那么可用的数据集 ?? 和其他相同的数据集可以从中采样。但是在实践中,不可能完美地近似数据 PDF,但是我们可以近似地近似它。这就是我们在机器学习中所做的一切。
现在让我们看看机器学习算法的元素,并使(Mitchell et al .,1997)给出的机器学习的模糊定义在数学上具体化。
在本节中,我们描述了适用于 1.2 节中简要讨论的所有机器学习范例的机器学习算法的基本元素。机器学习算法有四个关键组成部分,即数据、模型、损失函数和优化。或者,也可以使用正则化技术来提高模型的泛化能力,并平衡偏差和方差的权衡(见 1.5 节)。
请记住,在机器学习中,我们的主要目标是训练一个应该在看不见的数据上表现良好的模型,因为我们的训练数据集将不会包含用户未来生成的数据。
数据集中存在的数据充当机器学习模型的经验。当模型首次用随机参数值初始化时,它不知道如何很好地执行某项任务。这种知识是通过迭代地将模型暴露给数据而获得的(通常是小样本计数,也称为小批量)。随着模型经历更多的样本,它逐渐学会更准确地执行任务。
一个数据集仅仅是一个结构化的,通常是表格(或矩阵)形式的数据点排列。表 1-4 显示了一个数据集的任意例子。该数据集包含人的一些特征(或特性),其中每一行包含单个人的特性。每行包含某个人的身高(厘米)、年龄(岁)和体重(千克)值。注意,特征及其对应的目标可以是任意维的张量值(这里是 0 维,即标量变量)。
表 1-4
分别用 x 1 ,x 2 和 t 标量表示身高、年龄和体重的人的数据集。
|身高( x 1 )
|
年龄( x 2 )
|
重量( t )
|
| --- | --- | --- |
| One hundred and fifty-one point seven | Twenty-five | Forty-seven point eight |
| One hundred and thirty-nine point seven | Twenty | Thirty-six point four |
| One hundred and thirty-six point five | Eighteen | Thirty-one point eight |
| One hundred and fifty-six point eight | Twenty-eight | Fifty-three |
给定数据集,我们必须决定任务的特征和目标。换句话说,为一项任务选择正确的特征完全取决于我们的决定。例如,我们可以使用这个数据集来执行一个回归任务,根据一个人的身高和年龄来预测体重。在这个设置中,我们的特征向量 x 包含身高 x 1 和年龄 x 2 ,即x=【x1x2,对于每个人(称为样本),而目标 t 是 a 的权重例如,x=【136.5 18】和 t = 31.8 是给定数据集中第三人的特征向量和目标标量。
在机器学习文献中,模型的数据点输入也被称为示例或样本,其特征也被称为属性。例如,汽车的特征可以是颜色、轮胎尺寸、最高速度等等。另一个例子可以是药物,其特征可以包括化学式、每种化学元素的比例等等。目标,也称为标签或硬目标(当区别于软目标时),是对应于给定样本的期望输出。例如,给定图像的特征(像素值),目标可以是椅子、桌子等等,用向量表示。还要注意,对于数据集中的给定样本,所有目标始终保持不变。在极少数情况下,我们在半监督学习中为未标记的样本生成软目标,而在监督学习中目标总是被假定为不可变的。
1.4.1.1 设计矩阵
表示数据集最流行的方式是设计矩阵,如表 1-4 所述。设计矩阵是样本和目标的集合,每行包含一个样本(每列包含一个描述样本的特征)和相应的目标。目标值用于监督学习任务。只有样本包含特征而不是目标。目标是我们期望我们的模型预测给定样本特征的期望输出。
1.4.1.2 独立和相同的样本
一个好的数据集应该在统计上代表样本在数据生成概率密度函数中的总体分布。请记住,我们只能访问数据集,而不能访问 PDF。由于数据集在统计上代表一种概率分布,因此样本的分布方式总有一些模式。机器学习算法旨在发现数据集中的这种模式,以执行所需的任务。我们只能通过盯着一组样本,在低维(最多三维)上很容易地直观判断模式,但机器学习算法可以理解更高维(甚至数十亿)上的模式。例如,我们可以说“如果一个人的身高在[110,160]范围内,那么他的体重将在[30,80]范围内”,等等。但如果我们添加锻炼时间、营养摄入等特征,那么样本就会有更复杂的详细模式,这对我们来说可能很难集体处理,但机器学习算法可以为我们分析它,甚至更准确。
为了让任何机器学习算法在任务中表现良好,我们需要数据集上的两个约束来发现样本之间的模式。首先,每个样本的值应该独立于另一个样本,也就是说,样本不应该相关,尽管每个样本中的单个特征应该相关。第二,样本应该是相同的,也就是说,它们相应的特征应该是相似的,并且在分布上表现出一些模式。
也就是说,符合这种约束的自然照片的假想数据集可能包含河流、车辆、天空、水下生物、植物、人类、动物等的图像,其中每个样本都是一张照片,其特征是红、绿、蓝颜色组合的像素值。这满足了相同的要求,因为,例如,风景图像将总是包含天空和地面。此外,该自然数据集也符合独立约束,因为没有图像影响其他图像的特征(像素)值。这种数据集的一个很好的例子是 ImageNet (Russakovsky 等人,2015 年)。
1.4.1.3 数据集分割
现在我们知道了什么是数据集以及它是如何表示的,下一步是使用它来学习它在模型中的层次表示。但是在模型训练之前,数据集必须被分成多个子集。在训练机器学习模型之前,这是一个非常重要的步骤,原因将在下面讨论。
实际上,该模型通常有大量参数,很容易使整个数据集过拟合。通过过拟合,我们的意思是该模型在数据集上表现很好,但在现实世界中肯定会遇到的看不见的例子上表现很差。另一个术语是欠拟合,这意味着模型在它被训练的数据集或看不见的数据集上都表现不佳。欠拟合和过拟合之间的平衡是一个困扰整个机器学习领域的问题,也被称为偏差和方差权衡(参见 1.5 节)。
我们将整个数据集主要分成三个子集,即训练集、测试集和验证集。如果整个数据集包含具有相同 id 的示例,那么每个子集也将包含具有相同 id 的示例。这些子集在建立良好的机器学习模型中发挥着至关重要的作用,解释如下。
训练集包含用于调整模型可学习参数的示例和目标。该模型被训练以迭代地最小化给定输入特征样本的预测输出和期望目标值之间的误差。作为模型在看不见的例子上表现良好的先决条件,它最初应该在训练过程中被允许经历的训练集上表现良好。
测试集包含模型在训练过程中不允许经历的例子。这是唯一用于测试模型性能的。在现实世界中,测试集被精心设计为包含来自数据集的示例,这些示例通常很难很好地执行。这样做是为了选择更好的机器学习模型。测试集还可能包含机器学习模型在现实中可能经历的示例。我们通常更关心我们可能从用户那里期待的真实世界的数据,例如,智能手机拍摄的照片,而不是卡通人物的图像。所以我们的测试集应该包含智能手机点击的照片。我们想要的最终结果是,我们的模型能够在看不见的例子上产生更接近真实目标的良好预测。如果一个给定的模型在看不见的例子上表现很好,就说它有一个好的泛化特性——否则就是坏的。
验证集,也称为开发集,用于为机器学习算法选择一组可能的超参数配置、模型架构等。与测试集不同,验证集在训练过程中用于评估模型的性能。但是重用同一个验证集会导致机器学习算法过拟合。为了克服这个问题,研究人员有时会使用多个交叉验证集。然后在多个验证集上逐一评估机器学习算法,以评估其在未知示例上的准确性。
根据经验,数据集应该分为 70%的训练集和 30%的测试和验证集。但是如果数据集有大量的样本,那么您可能不需要遵循这个标准。方法应该是分割数据集,使其在准确性方面代表对错误分类示例的良好估计。有关更多细节,我们请读者参考(Ng,2018)中关于设计机器学习工作流的指南,主要用于工业应用的监督学习任务,而在本书中,我们的目标是向您介绍高级深度学习算法并对它们进行编程。
我们在上一节中讨论了数据集。目标是在机器学习算法中利用数据集,该算法学习对未知样本进行预测。为了实现这一点,我们需要一个机器学习模型。
在机器学习中,模型是一个具有可学习系数的数学函数。在本文中,函数的系数被称为参数。在训练之前,用小的随机参数值初始化机器学习模型。这些参数在优化阶段,也称为训练阶段期间缓慢变化。目的是有一个机器学习模型,在看不见的例子上表现良好。在推理阶段,机器学习模型被用于现实世界的应用中,在现实世界中,它会遇到在训练阶段没有看到的例子。
有两种广泛用于近似数据概率密度函数的模型,即参数模型和非参数模型。我们将在下文中简要讨论这些模型。
1.4.2.1 非参数模型
非参数模型使用整个数据集来预测给定测试样本特征的标签。他们使用一个核函数来衡量样本之间的相似性。对于所有训练示例和一个测试示例,该函数被迭代调用。核函数的选择在不同的核方法之间是不同的。例如,径向基核方法使用径向基函数;k-最近邻回归和分类方法使用诸如曼哈顿、欧几里德距离等函数。核函数也可以很容易地扩展,以产生一个神经网络。
对非参数模型的深入解释超出了本书的范围。我们建议您参考该文献中的(Bishop,2006)和(Murphy,2012)教科书。
1.4.2.2 参数模型
参数模型是包含可调系数(也称为参数)的函数。参数模型通过更新其参数值来执行任务。与总是使用整个数据集进行预测的非参数模型不同,参数模型只学习一次数据集的表示,并使用其参数中存在的知识进行预测。很难解释参数模型中存在的知识,这是一个活跃的研究领域。请参考(卡特等,2019;Olah et al .,2017,2018)对神经网络的特征进行深度可视化。非参数模型融合了训练和测试概念。参数模型有时训练很慢,但推理很快,也就是说,对于设备上或云上服务的用户来说,它们是实时部署的良好候选。
本书的主要焦点是在第五章中介绍的参数模型。在 1.1 节中,我们没有讨论模型如何学习。在下文中,我们将解释学习(或训练)过程。
损失函数计算预测值和目标值之间的距离。它通过找出预测值和目标值之间的距离来衡量模型在预测给定输入的正确输出方面有多好,其中距离的概念由基于预测分布的各种损失函数(见第 5.5 节)定义。注意,损失函数在其他教材中也被称为误差函数、代价函数、目标函数。在本书中,我们更喜欢损失函数这个术语。
在训练期间,损失函数将模型的可学习参数导向这些值,使得模型预测相应输入的期望输出。请注意,损失函数不能用作评估模型的性能指标。
对于回归任务,损失函数的最常见选择是由以下等式定义的误差平方和:
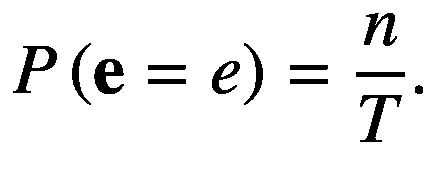
(1.6)
其中l(??; θ 为损失函数, y (i) 为输入样本的预测值x【I】,t(I)为其对应的目标值, θ 为可学习参数。数据集中总共有 N 个样本。该损失函数中的平方确保总损失保持非负。损失函数中的分数项有其自身的重要性,因为它将损失函数的导数简化如下:
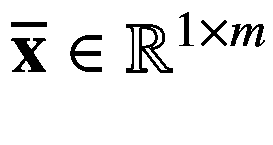
(1.7)
注意,一旦我们的模型被训练,我们将可学习参数表示为 θ* ,损失函数表示为l(??; θ* )或简单的 L ( θ* )保持抽象,对于数据集的哪个子集使用损失函数。
现在我们有了经验数据集和学习任务的模型,机器学习算法的最后一个组件是优化器(和可选的正则化器),它用于使模型从数据中学习,这将在接下来讨论。
优化,也称为训练,是使用损失函数更新模型的可学习参数,以最小化目标和预测之间的误差的过程。在训练期间,我们优化我们的机器学习模型,这是一个两步过程,即计算关于模型的每个可学习参数的误差梯度,并更新参数值。
在第一步中,我们计算损失函数相对于机器学习模型的每个可学习参数的梯度。为了完成这项任务,我们使用了一种称为误差反向传播 (Rumelhart 等人,1986 年)(也称为反向传播,或简称为反向传播)的高效算法。该算法只是微积分链式法则(见 2.3 节)计算梯度的连续应用。计算梯度的一个更通用的算法是自动微分(见 3.3 节),误差反向传播是它的一个特例。
在第二步中,我们使用在优化的第一步中获得的梯度信息来更新模型的参数。由于损失函数的梯度给出了其输出增加最多的方向,我们在梯度的负方向上以小步长迭代更新参数,因为我们的目标是最小化损失函数。用于优化的该参数更新步骤的学习算法被称为梯度下降,如以下等式所述:
(1.8)
这里, τ 表示优化过程的时间步长, θ ( τ ) 表示时间步长 τ 的参数值,同样 θ (τ+1) 表示时间步长τ+1 的参数值。术语?θ(τ)l表示在时间步长 τ 上用算法微分计算的关于权重参数 θ (τ) 的梯度。由于梯度值通常很大,我们必须采用超参数的小步长,用术语 η 表示,称为步长(或学习速率),以最小化损失函数,其中 η ∈ (0,1)。为了采取小的步骤,学习速率被乘以关于模型的每个参数的损失函数的负梯度。优化是一个连续的迭代过程,在每一步迭代中,参数 θ (τ) 被加上一个小步长更新—η?θ(τ)l以降低预测与目标之间的误差。
简而言之,单个训练步骤包括交替地向前传播输入特征信号,然后向后传播由损失函数计算和发出的误差信号。反向传播计算梯度,然后用于更新模型的参数。这种普通的梯度下降技术可能并不总是给出最好的结果。但是,正如在 5.6 节中详细描述的那样,对它还有各种各样的修改,以便进行更鲁棒的优化。
请注意,模型可能会遇到 1.5 节中讨论的过拟合和欠拟合问题。对于任何数据集的分割,如果达到这些状态之一,模型就不再有用。为了克服这些问题,通常在同一数据集上训练具有不同能力的不同机器学习模型。另一个解决方案是在训练模型时使用正则化技术,这将在接下来的第 5.7 节中详细讨论。
尽管正则化可能被认为是机器学习算法的可选元素,但它在训练更一般化的模型中起着重要作用。正则化是对数据、模型、损失函数或优化器进行的任何修改,以减少模型的泛化误差(即,模型应该具有低偏差和方差)。
这里,我们描述了损失函数的广泛使用的正则化项,称为 L 2 范数罚,或岭回归 (Hoerl & Kennard,1970),其将损失函数修改如下:
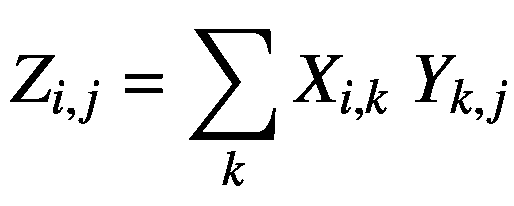
(1.9)
其中∩θ∩2计算参数的 L 2 范数, λ 表示正则项的权重,通常设置为 1。用这个新的损失函数训练模型有助于减少我们关心的泛化误差,也就是说,该模型将在看不见的样本上表现得更好。
在 5.7 节,我们将讨论各种其他的正则化技术。现在,让我们把注意力从训练模型转移到偏差和方差的概念上。
偏差和方差是不同数据集上模型性能的特征。偏差与训练集上的模型性能有关,而方差与验证集上的模型性能有关。我们希望找到一个低偏差和方差的模型。但是,实际上,我们通常用一种交换另一种。此外,偏差和方差权衡不仅影响传统的机器学习方法,而且困扰着整个机器学习领域。
在讨论偏差和方差的权衡之前,让我们先介绍一下泛化这个术语。如果该模型在看不见的数据点上表现得非常好,则称其具有良好的泛化特性。我们的目标是在机器学习中找到这样的模型。
主要有三种情况与模型的偏差和方差有关。虽然第四种情况(没有提到,但可以从其他三种情况推断出来)可能是可取的,但从统计上来看而不是是可能的,即使在理论上也是如此;否则,我们可能永远不会要求训练模型。
在第一种情况下,当模型在训练集上表现良好,但在多个验证集上表现不佳时,分别被称为具有低偏差和高方差。这意味着模型有足够数量的参数来很好地执行训练集,但它过拟合训练集(因为参数的数量超过了发现底层数据 PDF 的要求)或记住了训练集的映射,并且没有近似底层数据生成 PDF。这是因为如果它已经近似了数据分布,它也应该能够在验证集上表现良好,因为像训练集一样,验证集也在统计上表示数据 PDF。
在第二种情况下,当模型在训练集和多个验证集上都表现良好时,据说分别具有低 偏差 和低 方差。在这里,模型已经近似了基础数据 PDF,所有数据集都是出于训练和测试目的从该 PDF 中采样的。在实践中,我们努力寻找这种模式。
在第三种情况下,当模型在训练集和多个验证集上都表现不佳时,分别被称为具有高偏差和高方差。这里,模型没有足够数量的参数来近似训练集,因此,在多个验证集上也表现不佳。因为模型容量低,即使在训练集上表现也不好,所以据说欠适应。
我们讨论传统机器学习方法的各种问题,这些问题可以通过深度学习方法轻松解决。这激励我们研究和探索深度学习方法,正如我们将在下面看到的。
在实践中,我们通常会有几千甚至几百万个维度的样本。用传统的机器学习方法,如 k-最近邻回归器或分类器、决策树和其他方法处理这样的样本变得非常低效,有时甚至难以处理。
考虑设计机器学习算法的问题,该算法旨在近似可用数据集的映射。现在假设可用数据样本 x 的维数为 1,并且是标量变量,即 x ∈ ?.我们可以从用定积分区间划分输入的一维向量空间开始。而这样做,我们实际上是把输入向量空间分成了 M 这样的一维单元格(见图 1-3 (a))。我们可以在这条线上绘制训练集中的每个数据样本。我们需要在每个单元中至少有一个训练点,以便做出正确的预测。由于我们有每个样本的标签信息,当我们需要预测一个新的未知样本的标签时,我们可以简单地在这条线上绘制它,并将其分配给在该单元中具有最大计数的标签,用于分类任务。在回归的情况下,我们可以取训练点的所有实值标签的平均值,并将该值赋给这个测试样本。
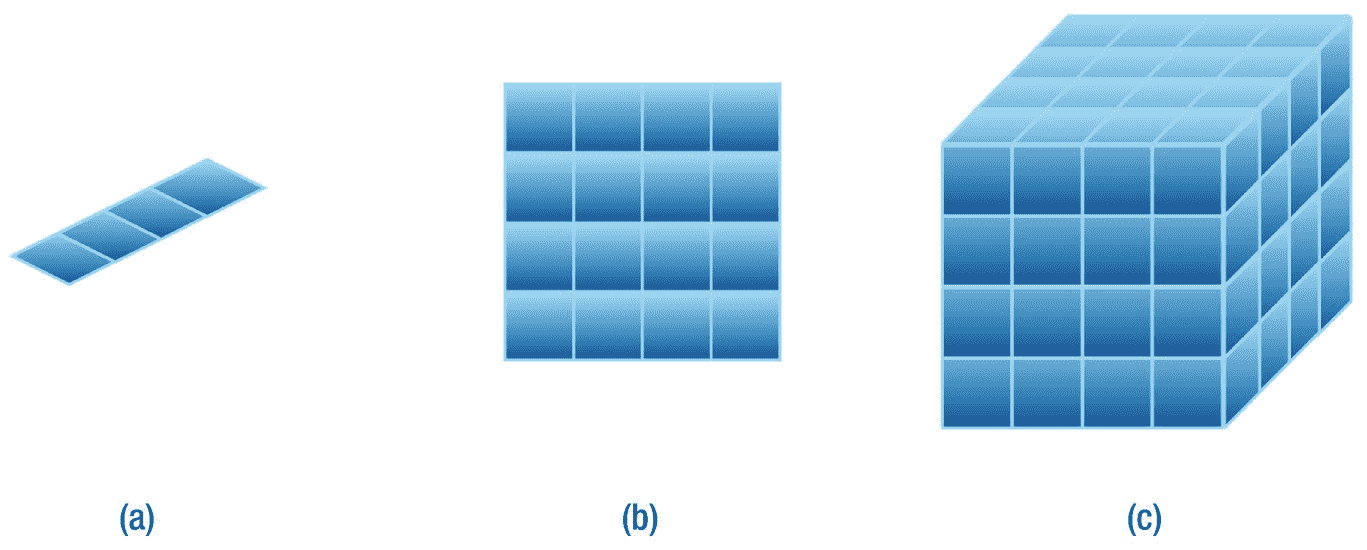
图 1-3
(a)一维、(b)二维和(c)三维数据点的维数灾难。存在对样本的指数要求 M d 用于预测新样本的标签,其中 M = 4 是沿着每个维度的部分的数量,而 d 是维度的数量。
在一维输入空间中工作似乎非常容易。但是当我们跳到更高维度的空间,我们开始看到问题迅速出现。现在假设变量 x ∈ ? 2 的二维输入向量空间由分别代表 x 轴和 y 轴的变量 x 1 和 x 2 组成。现在可以将每个训练点绘制为矩阵中的一个点。我们可以再次将 xx1 和 xx2 变量的 x 轴和 y 轴划分为 M 段,这样我们就得到了M2 单元格(参见图 1-3 (b))。我们可以使用前面描述的过程再次简单地预测这个测试样本的标签。当我们移动到三维向量空间 x ∈ ? 3 时,其中 x、y 和 z 轴分别由 x 1 、x2 和 x 3 变量表示,然后我们得到 M 3 截面(见图随着维数增加的趋势,我们可以看到训练集中所需的标记样本的数量随着维数的线性增加而呈指数增加。我们至少需要总共Md 个样本来近似数据集映射,其中 d 是样本特征空间的维度。维度和所需样本数量之间的这种指数关系被称为维度诅咒 (Bellman,2015)。
幸运的是,我们可以用深度神经网络模型解决维数灾难,我们将在本书后面看到。现在我们讨论传统机器学习算法的另一个问题,称为平滑度假设。
传统的机器学习算法假设输入变量值的微小变化不会导致预测输出变量值的突然变化。这被称为平滑度假设。这意味着对于任何两个相似的输入值(例如,看起来相似的图像),预测标签应该总是与真实标签相同。直观地说,这也适用于我们的视觉系统,因为当两幅图像相似或不相似时,我们可以区分它们。当我们的稀疏训练数据没有填满所有单元时,这种假设是有帮助的;然后,我们可以简单地将输入值插值到更接近可用训练样本的位置,并将相同的标签分配给我们的测试样本。
在(Szegedy 等人,2013 年)的工作之前,这种观点在很大程度上被认为对非线性方法有效。作者表明,我们可以有意构建看起来相似但被深度神经网络错误分类的输入图像。从几何学上来说,我们可以说这个假设是有效的,但只对线性模型有效,而对于非线性模型,这个假设不成立。但是,由于我们对处理高维数据感兴趣,因为它携带重要的信息,并且由于传统机器学习方法的弱表示能力,我们无法实现良好的准确性。这促使我们采用深度学习方法。
接下来,我们看看深度学习相对于传统机器学习方法所提供的一些优势。
正如我们之前讨论的,传统的机器学习方法存在各种问题。这阻碍了我们对高维数据的分析。如这里所讨论的,深度学习方法相对于传统的机器学习方法有各种优势。
与传统的机器学习方法不同,深度学习已知可以给出高度准确的结果,有时甚至在某些任务上超过人类水平的表现。深度学习的想法大致是受大脑神经系统处理直接从我们的世界获得的原始数据的方式的启发。类似于我们的眼睛和耳朵等感觉器官在发送到大脑之前对数据进行预处理的事实,我们有时也会在将数据用于深度学习模型之前对数据进行预处理,但这种预处理使用了完全不同的功能序列。但是请注意,关于大脑本身,我们还有许多事情不知道。深度学习方法使用原始数据作为输入样本,并对其进行处理,以学习内部分层高维空间中的抽象信息。我们不需要为模型选择重要的特征。因为选择过程在人类中是固执己见的,一些人会发现某一组特征对任务很重要,而另一些人会更喜欢其他一些特征。深度学习通过简单地处理原始数据本身来解决这个特征手工制作问题。深度学习中的模型具有多层类似神经元的功能,其中每层通常具有不同的维度。高维输入进入模型,并在不同的层中转换成不同的维度,直到生成预测输出的最后一层。承担图像分类的任务。在这里,初始图层(更接近输入)可能会从影像数据集中学习精细比例的细节,如边缘、颜色梯度等,而中间层(称为隐藏图层)可能会学习更粗糙比例的细节,如圆形、矩形等形状;靠近最后一层的层(称为预测层)可以学习眼球、身体形状等特征;然后最终预测层将预测给定图像样本的标签。深度学习中的这些模型有许多名称,如深度学习模型、人工神经网络、深度神经网络或简单的神经网络,名称的列表还在继续。第五章致力于介绍神经网络和训练它们的各种成功技术。
我们还注意到,从随机存取存储器(RAM)和计算速度的角度来看,当我们有大量样本并且每个样本都可以在大维度上表示时,传统方法有时是难以处理的。深度学习模型利用了并行处理比顺序处理快得多的事实。这些模型并行处理样本的特征。虽然机器学习在 2006 年复兴(Bengio et al .,2007;Hinton 等人,2006 年;Ranzato 等人,2007 年),大约在 2009 年,很明显图形处理单元(GPU)可以加速深度学习模型(刘冰等人,2009 年),甚至比中央处理单元(CPU)设备快 10 或 20 倍,用于训练和推理过程。从那以后,像 Nvidia 这样的公司已经投入了极大的努力 2 来构建更快的 GPU,并不断改进架构设计。谷歌也在努力建造更快的并行处理设备,他们称之为张量处理单元(TPUs)。云甚至边缘设备上都有 TPU。在撰写本文时,著名的平台即服务(PaaS)如 Google Colaboratory 和 Kaggle 提供了对云上 GPU 和 TPU 设备的免费访问,用于深度学习。这有助于极大地加速深度学习研究。这本书里写的所有代码都可以在 Google Colaboratory 平台上执行。
深度学习方法可以被认为是传统机器学习方法的继承者,因为它们具有各种有趣的优点。几乎本章中针对传统方法(除了非参数方法)讨论的每个想法和概念都可以移植,而几乎不需要对深度学习框架进行任何修改。从根本上说,深度学习的定义保持不变:最大似然估计的思想非常适合,因为深度学习模型本质上是参数模型,深度学习也需要 1.4 节中讨论的学习算法的所有元素,并且每种类型的机器学习都可以用深度学习方法来执行(并且更好)。我们将从第五章开始,用简单的神经网络深入研究深度学习。
本章介绍了与机器学习相关的基本概念。我们讨论了机器学习的各种范例,并介绍了帮助训练机器学习模型的最大似然估计的概念。然后,我们深入研究了机器学习算法的各种基本元素。我们还引入了偏差和方差的概念来理解模型的泛化特性。最后,我们揭示了深度学习方法相对于传统机器学习方法的优势。
我们将在以下章节中从基本概念开始研究深度学习。但在深入之前,在下一章,我们将研究不同数学分支的各种主题,这些主题对于理解深度学习是必不可少的。
世界上发生的任何事情,其意义都不是某种最大值或最小值。
—莱昂哈德·欧拉
本章介绍了理解神经网络基础所必需的数学知识。我们强调,如果你的数学概念生疏了,不要跳过这一章。学习后面的章节时,你可以参考这一章。
在第 2.1 节中,我们介绍了线性代数,它用于利用神经网络进行预测,并计算损失函数相对于神经网络的梯度,这使得学习成为可能。线性代数运算的有效实现,如基本线性代数子程序(BLAS),也允许在现代硬件加速器如 GPU 上使用并行处理进行快速计算。线性代数在设计神经网络的结构中也起着重要的作用。神经网络可被视为一个概率框架,用于近似可用数据集的概率分布(第 1.3 节),这需要理解第 2.2 节中讨论的概率论。与确定性编程不同,神经网络的概率方法使其在处理值可能在连续空间中变化的输入数据时具有鲁棒性。在第 2.3 节中,我们引入了微分学来计算神经网络损失函数的梯度,这有助于确定如何训练神经网络。
本节介绍不同的矩阵和向量,重要的一元和二元矩阵运算,以及规范。这些数据结构概括在张量的概念下,在 4.1 节中讨论。
有各种类型的矩阵和向量,但我们将自己限制在深度学习领域中重要的那些。我们首先介绍不同的矩阵,然后讨论一些重要的向量。
当一个方阵(具有相同的行数和列数)沿主对角线的所有属性都为 1 时,该矩阵称为单位矩阵,用 I n 表示,其中In∈?n×n表示例如,5 阶的单位矩阵被写成如下:
![$$ left[begin{array}{l}1kern0.5em 0kern0.5em 0kern0.5em 0kern0.5em 0 {}begin{array}{cccc}0& 1& 0& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}0& 0& 1& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}0& 0& 0& begin{array}{cc}1& 0end{array}end{array} {}begin{array}{cccc}0& 0& 0& begin{array}{cc}0& 1end{array}end{array}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402862.png)
(2.1)
我们还可以找到一个给定矩阵的逆矩阵,用A?? 1 表示,其中 A 是可逆矩阵。逆矩阵由下面的等式定义:
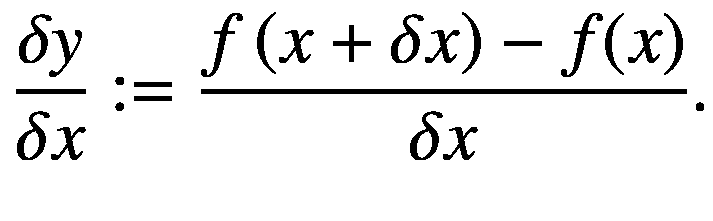
(2.2)
其中I??n是一个 n 阶单位矩阵。注意,矩阵 A 必须是可逆的,以产生其逆矩阵A1。
对角矩阵 D 定义为除了 i = j 之外所有元素为零的矩阵。例如,下面是一个对角矩阵:
![$$ left[begin{array}{l}2.5kern0.5em 0kern0.86em 0kern0.5em begin{array}{cc}0& 0end{array} {}begin{array}{cccc}kern0.48em 0& 8& kern0.36em 0& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& -3& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& kern0.36em 0& begin{array}{cc}4& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& kern0.36em 0& begin{array}{cc}0& 5end{array}end{array}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402802.png)
(2.3)
我们可以通过使用 diag(.)运算符。如果我们的矩阵是 D,那么 diag( D )返回一个向量 x ,包含沿着 D 主对角线的元素,如下:
![$$ mathbf{x}=left[begin{array}{l}2.5 {}kern0.36em 8 {}-3 {}kern0.36em 4 {}kern0.36em 5end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402602.png)
(2.4)
当我们转置一个矩阵 S 并得到相同的矩阵时,那么这种矩阵称为对称矩阵。从形式上来说,对称矩阵是其转置返回相同矩阵的矩阵,即ST=S:
![$$ mathbf{S}=left[begin{array}{l}0kern0.5em 8kern0.5em 5kern0.5em begin{array}{cc}6& 2end{array} {}begin{array}{cccc}8& 4& 3& begin{array}{cc}7& 9end{array}end{array} {}begin{array}{cccc}5& 3& 7& begin{array}{cc}1& 1end{array}end{array} {}begin{array}{cccc}6& 7& 1& begin{array}{cc}3& 6end{array}end{array} {}begin{array}{cccc}2& 9& 1& begin{array}{cc}6& 5end{array}end{array}end{array}
ight]={mathbf{S}}^T $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402722.png)
(2.5)
在前面的等式中,矩阵 S 是对称的,因为它等于它自己的转置。
我们现在介绍一些在深度学习中有意义的向量。假设两个向量 u 、v∈Rn使得uTv= 0,假设这两个向量都是非零向量,则称为正交向量。当一个向量的欧氏范数为 1 时,则称为单位向量,即∨u∨2= 1。现在我们假设两个向量 u 和 v 也是单位向量;那么这两个向量被称为正交向量。形式上,当两个单位向量在性质上正交时,那么它们被简单地称为正交向量。
我们介绍一些适用于矩阵的一元算子。转置是神经网络中对矩阵常用的一元运算之一。矩阵 B 的转置给出一个新的矩阵 A ,其行元素被其自己的列元素交换,使用以下规则:
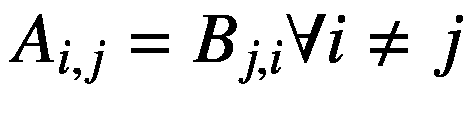
(2.6)
例如,假设对以下具有不同行数和列数的非对称矩阵进行转置:
![$$ mathbf{S}=left[begin{array}{l}-2kern0.5em 0kern0.5em 5 {}begin{array}{ccc}kern0.36em 4& 2& 9end{array}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402902.png)
(2.7)
![$$ {mathbf{S}}^T=left[begin{array}{c}-2kern0.5em 4 {}begin{array}{cc}kern0.24em 0& 2end{array} {}begin{array}{cc}kern0.24em 5& 9end{array}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402772.png)
(2.8)
可以清楚地看到,行与它们对应的列进行了互换,即矩阵 S ∈ ? 2×3 ,而其转置st∈?3×2。另一种算子称为对角线算子,用 diag(.),前面讨论的也是一元运算符的例子。如果需要计算所有主对角线条目的总和,那么我们使用 Tr(.).数学上用以下等式描述:
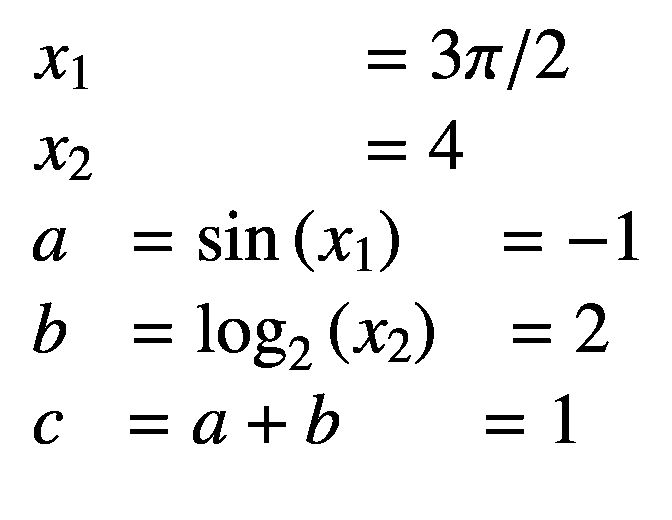
(2.9)
在我们之前考虑过的对角矩阵 D 上应用追踪算子给出如下:
![$$ mathbf{D}=left[begin{array}{l}2.5kern0.5em 0kern0.86em 0kern0.5em begin{array}{cc}0& 0end{array} {}begin{array}{cccc}kern0.48em 0& 8& kern0.36em 0& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& -3& begin{array}{cc}0& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& kern0.36em 0& begin{array}{cc}4& 0end{array}end{array} {}begin{array}{cccc}kern0.48em 0& 0& kern0.36em 0& begin{array}{cc}0& 5end{array}end{array}end{array}
ight],mathbf{x}=left[begin{array}{l}2.5 {}kern0.36em 8 {}-3 {}kern0.36em 4 {}kern0.36em 5end{array}
ight],s=sum limits_i{x}_i=16.5 $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402702.png)
(2.10)
通过对沿着矩阵 D 的主对角线的元素求和,我们得到总和等于 16.5。
我们针对两种特殊情况介绍了一些重要的矩阵二元运算:一个操作数是矩阵,另一个是标量,两个操作数都是矩阵。这种分类简化了对矩阵上二元运算的理解。
一些最简单的矩阵运算是矩阵和标量之间的运算。假设一个标量 s 和矩阵 A ∈ ? m×n 产生另一个相同形状的矩阵b∈?m×n,当某个运算符作用于操作数 s 和 A 之间时。这里,运算符可以是任何基本运算符,如加、减、乘或除。当在 s 和 A 之间应用这些操作符中的任何一个时,则 s 和 A 的每个元素之间会单独发生一次操作。例如,加法运算可以写成:
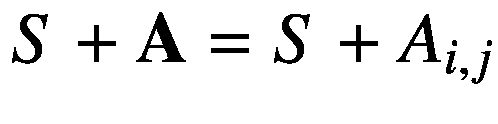
(2.11)
假设矩阵 A ∈ ? 2×2 和标量s= 3:
![$$ mathbf{A}=left[begin{array}{cc}1& 5 {}4& 9end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402572.png)
(2.12)
![$$ smathbf{A}=3;left[begin{array}{cc}1& 5 {}4& 9end{array}
ight]=left[begin{array}{cc}3.1& 3.5 {}3.4& 3.9end{array}
ight]=left[begin{array}{cc}3& 15 {}12& 27end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402992.png)
(2.13)
这里,为了简单起见,我们用点来表示标量之间的乘法。注意标量 s 乘以矩阵 A 的每个元素。
讨论了标量和矩阵之间的运算后,我们现在介绍两个矩阵之间最重要的运算之一,称为矩阵乘法。这是允许神经网络在现代并行处理硬件加速器上有效工作的基本操作。
让我们假设两个矩阵x∈?m×n和y∈?n×o相乘在一起产生一个新的矩阵z∈?m×o。 X 和 Y 的矩阵乘法简单写成 Z = XY 。这些矩阵必须满足某些条件,它们之间的乘法运算才有效。我们要求 X 的列数必须等于 Y 的行数,这在相乘后导致矩阵 Z 的行数和列数分别等于 X 和 Y 的行数和列数。形式上,两个矩阵之间的乘积定义如下:
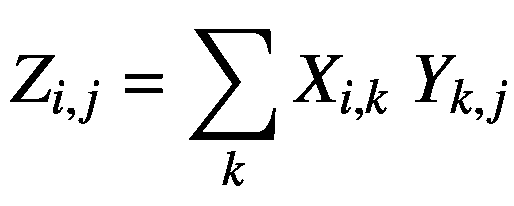
(2.14)
这里, i 、 j 和 k 是从 1 开始直到它们的维度大小的索引——分别定义变量 m 、 n 和 o 。对于矩阵 X 和 Y ,我们假设 m = 2, n = 3, o = 2。通过在它们之间应用矩阵乘法,我们得到 Z ∈ ? 2×2 如下:
![$$ mathbf{X}=left[begin{array}{cc}1& 6kern0.5em 2 {}3& begin{array}{cc}1& 4end{array}end{array}
ight],mathbf{Y}=left[begin{array}{c}begin{array}{cc}5& 1end{array} {}begin{array}{cc}2& 2end{array} {}begin{array}{cc}3& 2end{array}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402682.png)
(2.15)
![$$ mathbf{Z}=left[begin{array}{cc}1.5+6.2+2.3& 1.1+6.2+2.2 {}3.5+1.2+4.3& 3.1+1.2+4.2end{array}
ight]=left[begin{array}{cc}23& 17 {}29& 13end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402432.png)
(2.16)
前面的例子显示了 X ∈ ? 2×3 和 Y ∈ ? 3×2 之间的矩阵乘法返回 Z ∈ ? 2×2 。还要注意,矩阵乘法 YX 是不可能的,因为它不满足矩阵乘法的维数要求。因此,矩阵乘法不是交换运算。
请注意,矩阵乘法只是左侧矩阵的行和右侧矩阵的列之间的点积的重复应用。这也是为什么在一些像 NumPy 这样的库中找到一个名为的函数是非常常见的,而另一些像 Swift for TensorFlow 将其命名为。
矩阵之间还存在另一种乘积,称为按元素的乘积或 Hadamard 乘积,由 P = Q ⊙ R 表示,但是在用于 TensorFlow 的 Swift 中,我们使用*运算符来表示相同的乘积。这里,我们要求 Q 和 R 必须具有相同的形状,并且 Hadamard 运算产生一个与 Q 或 R 形状相同的 P 矩阵。它由下列等式给出:
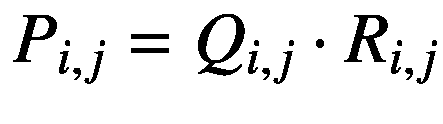
(2.17)
下面给出了一个基于元素的产品的实例:
![$$ mathbf{Q}=left[begin{array}{cc}1& 3 {}2& 4end{array}
ight],mathbf{R}=left[begin{array}{cc}6& 9 {}4& 1end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402842.png)
(2.18)
![$$ mathbf{P}=mathbf{Q}odot mathbf{R}=left[begin{array}{cc}1.6& 3.9 {}2.4& 4.1end{array}
ight]=left[begin{array}{cc}6& 27 {}8& 4end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402292.png)
(2.19)
哈达玛乘积生成与 Q 和 R 形状相同的矩阵 P 。
在深度学习中,有时可能需要测量向量的大小。为了完成这个任务,使用了一个叫做 norm 的函数。范数在 p 维向量空间中测量向量离原点的距离。向量的范数由 L p 或∨x∨p表示,并使用以下公式计算:
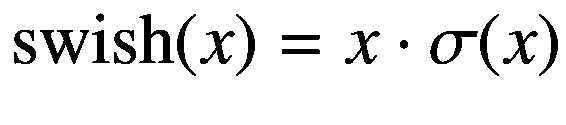
(2.20)
其中 p 必须满足条件 p ≥ 1。
有些规范在深度学习中是如此的司空见惯,以至于有了自己的名字。欧几里德范数或L2范数就是这样一个例子,其中 p = 2,它测量一个向量离原点的欧几里德距离。另一种感兴趣的定额是L1定额其中 p = 1。它还测量到原点的距离,但在零值和非常小的非零值之间的差异很重要的情况下,它更有帮助。如果我们向向量的每个元素添加一个小的非负值 e ,那么 L 2 范数与它自身的平方成比例地增加,但是当非常小的变化具有高显著性时, L 1 范数优于 L 2 。
在下一节继续讨论概率论之前,我们再讨论两个范数:max 范数和 Frobenius 范数。 max 范数表示为 L ∞ 简单来说就是向量中一个元素的最大幅度的绝对值,其写法如下:
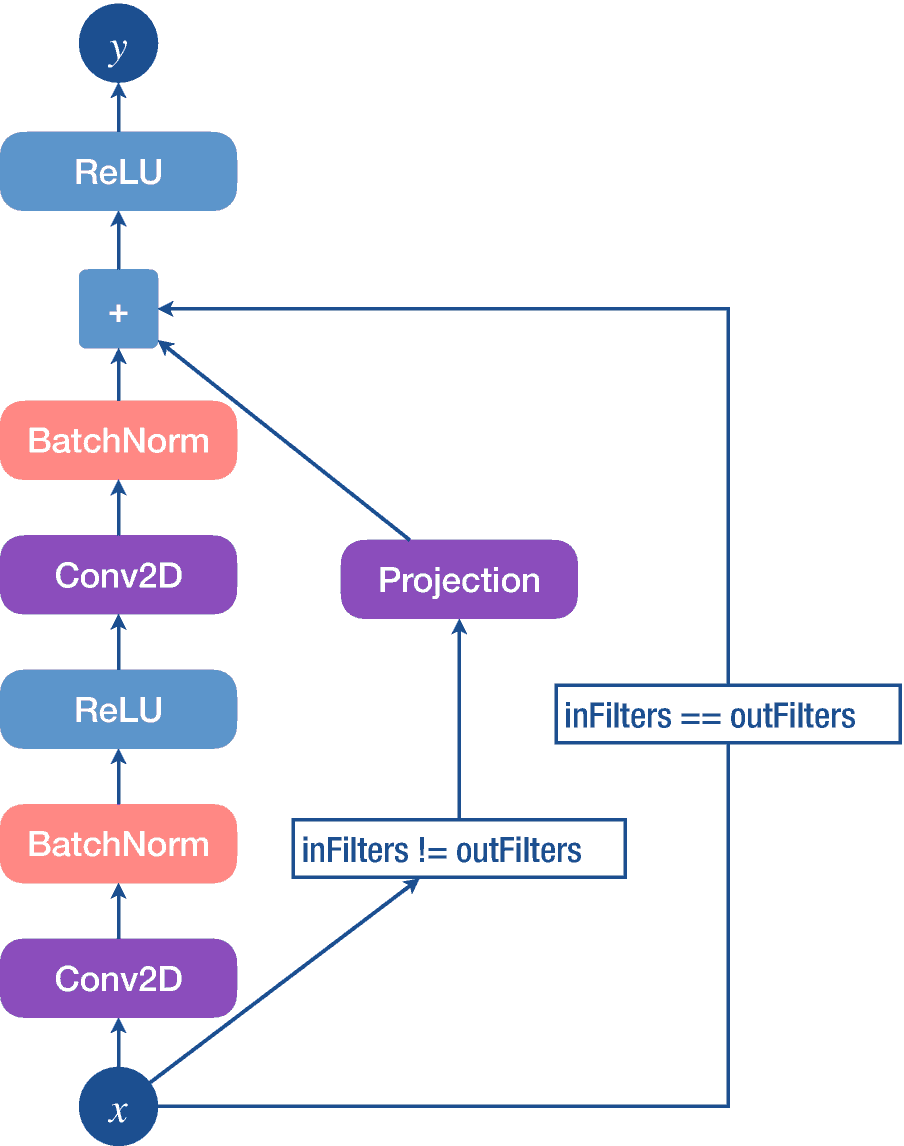
(2.21)
最后,我们还可以使用 Frobenius 范数来度量矩阵到原点的距离。它类似于向量的 L 2 范数。但很少使用,写如下:
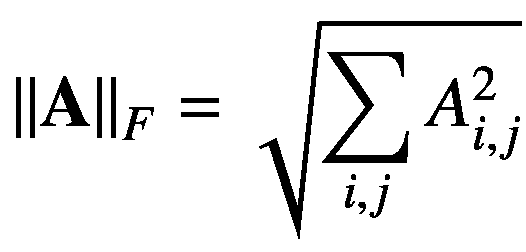
(2.22)
现在让我们熟悉一下与神经网络有关的另一个重要的数学分支——概率论。
深度学习就是对看不见的数据点做出决策,因为现实世界是高度不确定的。例如,一些不确定性在于确定事件的发生,例如“你将在明天早上 5 点醒来”或“这场音乐会将会很好”这些都是不确定的事件,因为它们可能会发生,也可能不会发生;因此,它们出现的概率在[0,1]范围内。相比之下,有些事件是完全肯定会发生的,例如,“太阳明天会升起”或“水是由氢和氧组成的”,所以它们的概率是 1。从未发生的事件,例如,“蓖麻油比水更粘”或“植物不在土壤中生长”,其概率等于 0。概率论在构建深度学习问题中起着至关重要的作用。
概率是一个数学框架,用于使用位于[0,1]范围内的实数来量化不确定事件。如果一个事件 e 有很高的发生概率,那么它的概率用一个更接近于 1 的实数来量化,而一个最不可能的事件有更接近于 0 的概率。形式上,一个事件 e 的概率,用 P ( e )表示,定义为无限次实验时,事件 e 发生的次数与总试验次数 T 的比值, T → ∞。概率中的另一个重要术语是随机变量,它被定义为可以从一组定义的有效值中取一个特定值的变量,其中每个值都有可能从给定的概率分布中被采样。这里, e 是随机变量;并且,从数学上讲,一个事件发生的概率 e 写成如下:
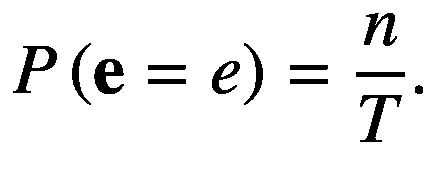
(2.23)
这里, e 是随机变量 e 发生的事件或值, n 是实验进行 T → ∞次时发生事件 e 的次数。注意,有时我们简单地把 P ( e )写成相当于把P(e=e)。也不要混淆概率论中的粗体小写字母符号和线性代数中的向量符号。这里使用这种符号是为了方便。
我们现在将使用一个简单的例子,以通俗易懂的方式解释概率论的基础知识。下面这个例子,如图 2-1 所示,改编自(Bishop,2006)教材的课本。让我们假设一个随机变量,我们称之为一天中的时间段,用 t = { m,a,e,b 表示,读作“ t 是一组值 m,a,e,和 b ,其中 m,a,e,和 b 分别代表早晨、下午、晚上和就寝时间。基于从 t 采样的值,我们可以决定采取由集合 a = { s,p,r,w 表示的动作,其中 s,p,r,和 w 分别简单地表示学习、玩耍、休息和锻炼。图 2-1 为随机变量 t 和 a 的示意图。
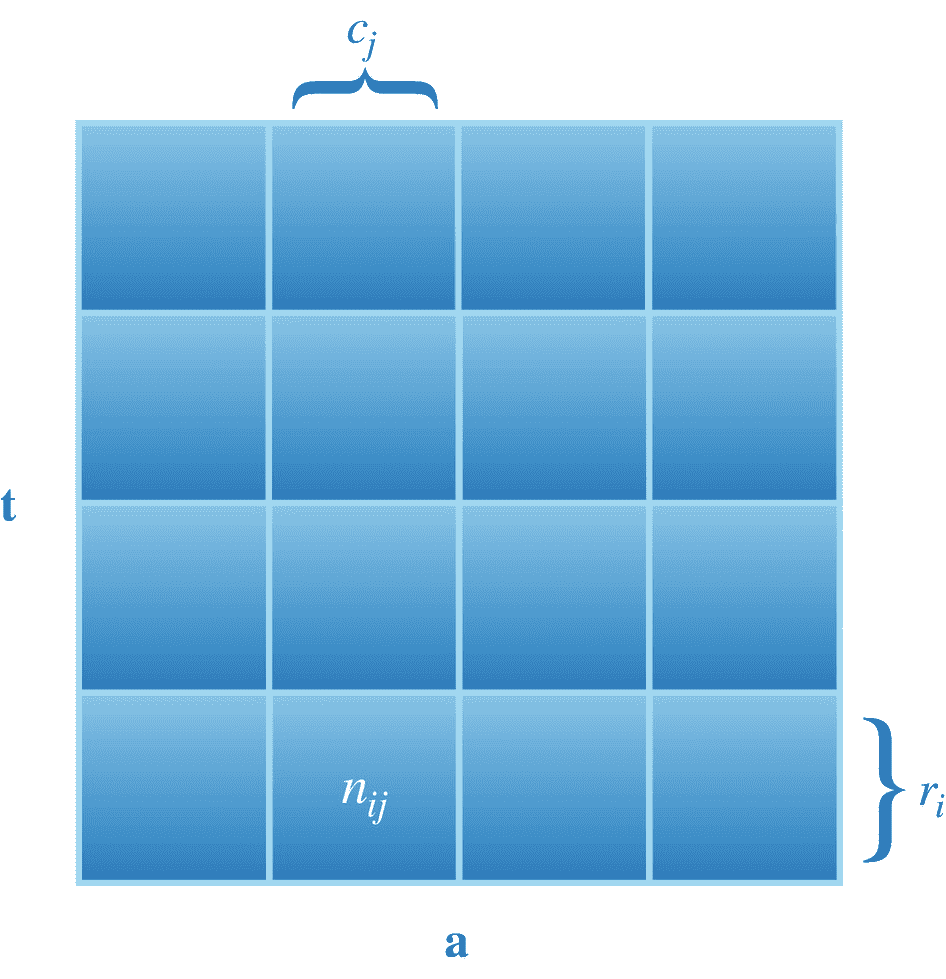
图 2-1
描述集合 t = {m,a,e,b}和 a = {s,p,r,w}中事件联合和有条件发生的概率的网格
在图 2-1 中,每行代表从 t 可以取的事件集{ m,a,e,b 中采样的第 i 个指标值,每列代表从 a 可以取的事件集{ s,p,r,w 中采样的第 j 个指标值。术语 r i 和 c j 分别表示事件实例的数量 t i 和 a j 。这里, i = 1、…、 M 和 j = 1、…、 N 分别是沿行和列的索引, M = N = 4。我们用P(t=tI)来表示一个事件发生的概率tI,它简单地由下面的等式给出:
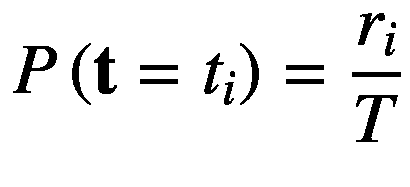
(2.24)
这里, T 是执行的实验总数。同样,事件发生的概率aj由
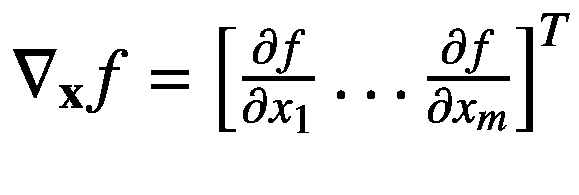
给出(2.25)
随机变量 t 采样值tI和 a 采样值 a j 时的概率,用P(a=aj,t=事件 t
注意,任意数量的随机变量的联合概率是对称的;因此,P(a=aj,t=ttI)与写作P(t=ttI,a
**### 条件概率
在给定另一个事件已经发生并且这两个事件相关的情况下,当我们必须找到一个事件的概率时,那么这种概率被称为条件概率。按照我们的例子,让我们假设 t 已经发生并取值tI;而给定这个,我们就要求 a 取值 a j 的概率。这用P(a=aj|t=tI)来表示, 读作“事件发生的概率 a j 假定事件 t i 已经发生”,并由单元格中实例数在第( i , j 个索引处的比率给出,用nij表示 形式上,这由下面的等式给出:
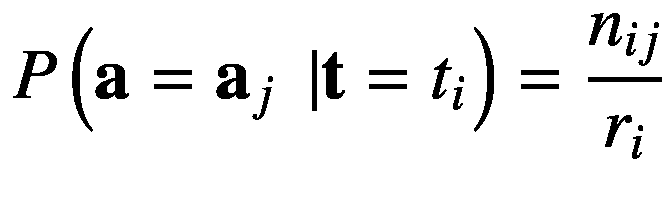
(2.27)
类似地,假定aj已经发生,事件tI发生的条件概率由nij与由 c j 给出的 j 列中事件总数的比值给出。形式上,P(t=tI|a=aj)由以下等式描述:
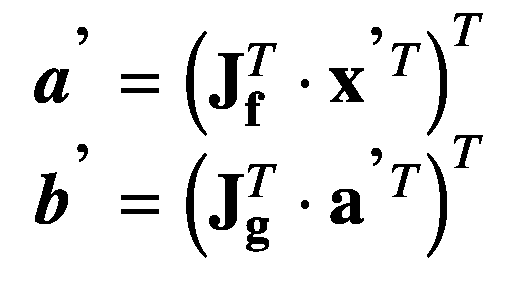
(2.28)
现在我们已经充分掌握了各种概率的知识,利用这些知识,我们将推导出概率论的两个基本规则,即和与积规则。首先,参见图 2-1 中的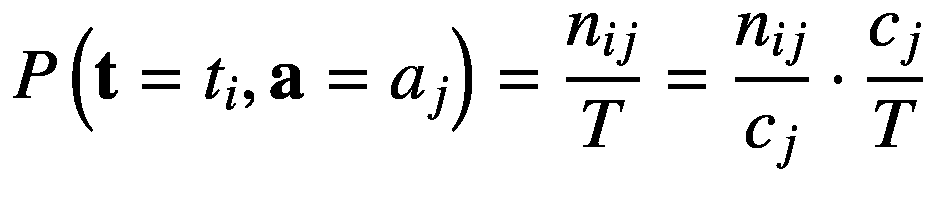 ,因为 r * i * 中的事件总数仅仅是该行每个单元格中所有事件的总和。使用等式 2.24 和 2.26 ,我们得到
,因为 r * i * 中的事件总数仅仅是该行每个单元格中所有事件的总和。使用等式 2.24 和 2.26 ,我们得到
(2.29)
这被称为概率的和。它也被称为边际概率,因为它是通过将所有变量边缘化或求和得到的,除了这里期望的一个变量,即 t 。同样,我们可以把P(a=aj)写成
(2.30)
通过边缘化随机变量 t 。接下来,我们将使用已经讨论过的条件概率来推导概率的乘积规则。利用等式 2.26 、 2.28 和 2.30 ,我们得到
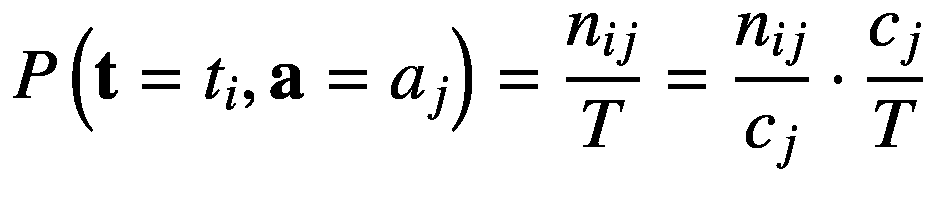
(2.31)
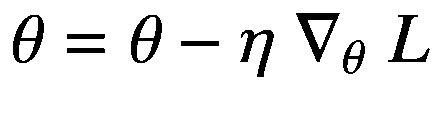
(2.32)
这叫做概率的乘积法则。请注意,它只是将两个随机变量的联合概率分解为它们的边际概率和条件概率的乘积。
到目前为止,我们已经对符号非常精确了,但是它使更大的方程变得复杂,并且降低了它们的适用性。我们现在选择一种更简单的符号来表示这样的概率方程。让我们将随机变量 t 和 a 的概率分布分别表示为 P ( t )和 P ( a ),而P(tI)和P(aj】现在我们可以更简洁地重写等式 2.30 和 2.32 如下:
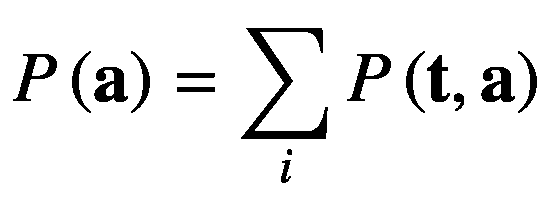
*(2.33)
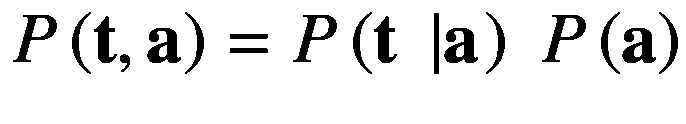
(2.34)*
这里,方程 2.33 和 2.34 分别代表概率的和与积法则。我们现在将在下文中介绍概率链规则的概念。
现在我们知道,两个随机变量的联合概率可以分解为它们的条件概率和边际概率的乘积。但是“如果我们想要分解两个以上随机变量的概率呢?”这就是概率链式法则的作用。概率的链规则被简单地定义为在尽可能多的随机变量上重复应用联合概率的乘积规则。因此,联合概率被分解为所有随机变量的边际概率和条件概率的乘积。
我们假设四个随机变量,分别是, x 1 、 x 2 、 x 3 、 x 4 。我们可以将它们的联合概率写成P(x1, x 2 , x 3 , x 4 )可以使用如下等式描述的乘积法则进一步分解:
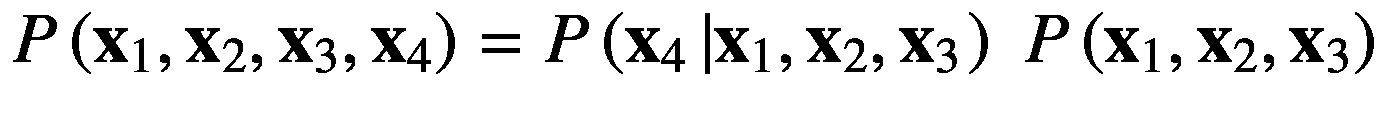
(2.35)
)
使用等式 2.36 和 2.37 ,等式 2.35 可以以其分解形式重写如下:
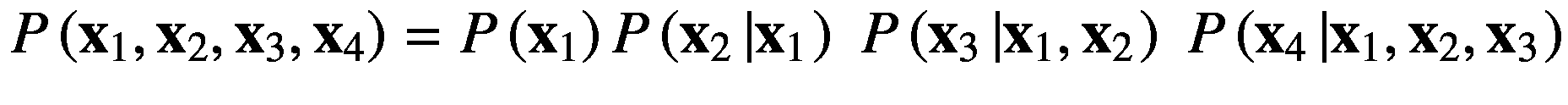
(2.38)
概率的链式法则的一般公式可以写成:

(2.39)
切记P(x|x)=P(x)。前面演示链式法则的例子可能看起来有点复杂;因此,让我们假设一个更简单的版本,它通过选择随机变量的名称来简化,即 a 、 b 、 c 和 d 。
我们现在将在这些随机变量上分解这个概率分布,这些随机变量由 P ( a , b , c , d )表示,在下面的等式中一步一步地分解:
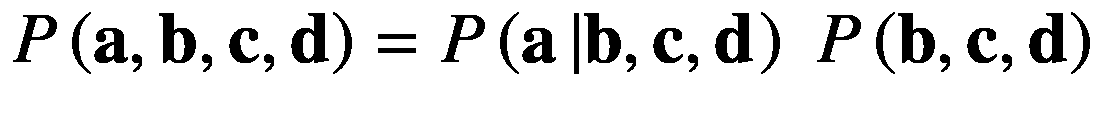
(2.40)
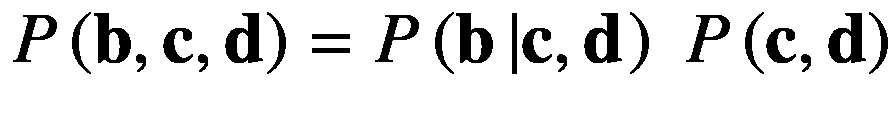
(2.41)
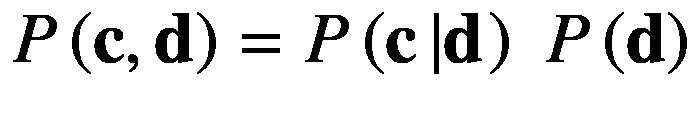
(2.42)
将方程 2.42 代入 2.41 中,然后将 2.41 代入 2.40 中,得到
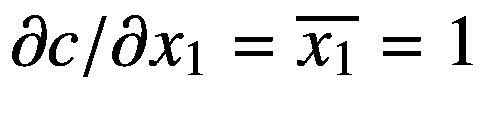
(2.43)
注意,分解后的方程 2.38 和 2.43 是对称的。简而言之,概率链规则帮助我们将任意数量的随机变量的联合概率描述为它们的条件概率和边际概率的乘积,并且更一般地通过等式 2.39 获得。
我们还可以利用联合概率是对称的这一事实来推导两个随机变量的条件概率之间的关系。我们可以将随机变量 x 和 y 的联合概率重写为
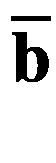
(2.44)
利用乘积法则,我们得到
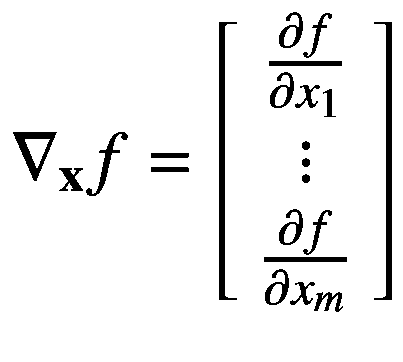
(2.45)
这里,等式 2.45 被称为贝叶斯规则,其通过联合概率的对称性质来关联条件概率。
微积分分支分为两个子分支,即微积分。因为神经网络训练需要计算偏导数,所以学习微分学是很重要的,也是本节的主题。我们不关心积分。我们先介绍函数的概念,然后解释微分学。本节受(Deisenroth 等人,2020 年)教科书第五章的启发。
微积分的核心是函数的概念。数学函数,表示为 f : ?? → ??,是从集合??到集合??的映射,将??的每个元素关联到??.的唯一元素假设变量 x ∈ ??和y∈??;那么y=f(x)就是将单个元素 x ∈ ??映射到唯一元素 y ∈ ??.的函数 f 换句话说,函数 f (。)转换输入 x 并返回输出 y 。
2.3.1.1 一元函数
当输入变量 x 到函数 f (。)是一个标量,并且函数返回一个标量输出 y ,那么这个函数被称为单变量(或者标量 ) 函数,如图 2-2 所示。换句话说,一元函数只是一个从标量实数到标量实数的映射, f : ? → ?.
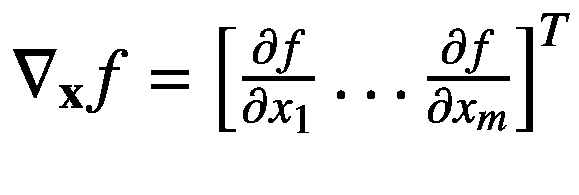
图 2-2
标量函数 f(。)从 x ∈ ?到 y ∈ ?的映射
考虑一个标量函数 g :从集合??到集合?的?? → ?映射,并取函数 f 的输出。)作为其输入,即z=g(y)=g(f(x))。这可以被视为多个函数的顺序链接,其中的 g 也被称为复合函数,如图 2-3 所示。我们也可以把复合函数写成g°f(x)其中°算子表示 g (。)和 f (。)功能。注意,函数的链接可以存在任意多的函数。我们将在后面看到,神经网络只是简单的复合向量函数。

图 2-3
复合标量函数 g ° f(x)映射
2.3.1.2 多元函数
前面描述的一元函数是函数的最简单形式。但是在深度学习中,我们会要求处理高维输入变量的函数。我们可以把这个定义扩展到一个输入包含多个变量的函数,这个函数叫做多元函数(如图 2-4 定义为 f : ? m → ?其中输入变量x∈?m(行向量)。一个真实世界的例子是速度 s ( d , t ),它是两个变量的函数,即距离 d ∈ ?和时间 t ∈ ?,定义为 s ( d ,t)=d/t我们可以将这两个输入变量表示为一个二维行向量 x = d t 变量。另一个例子是求和运算符σII,它返回一个向量 x 的所有标量元素之和。**
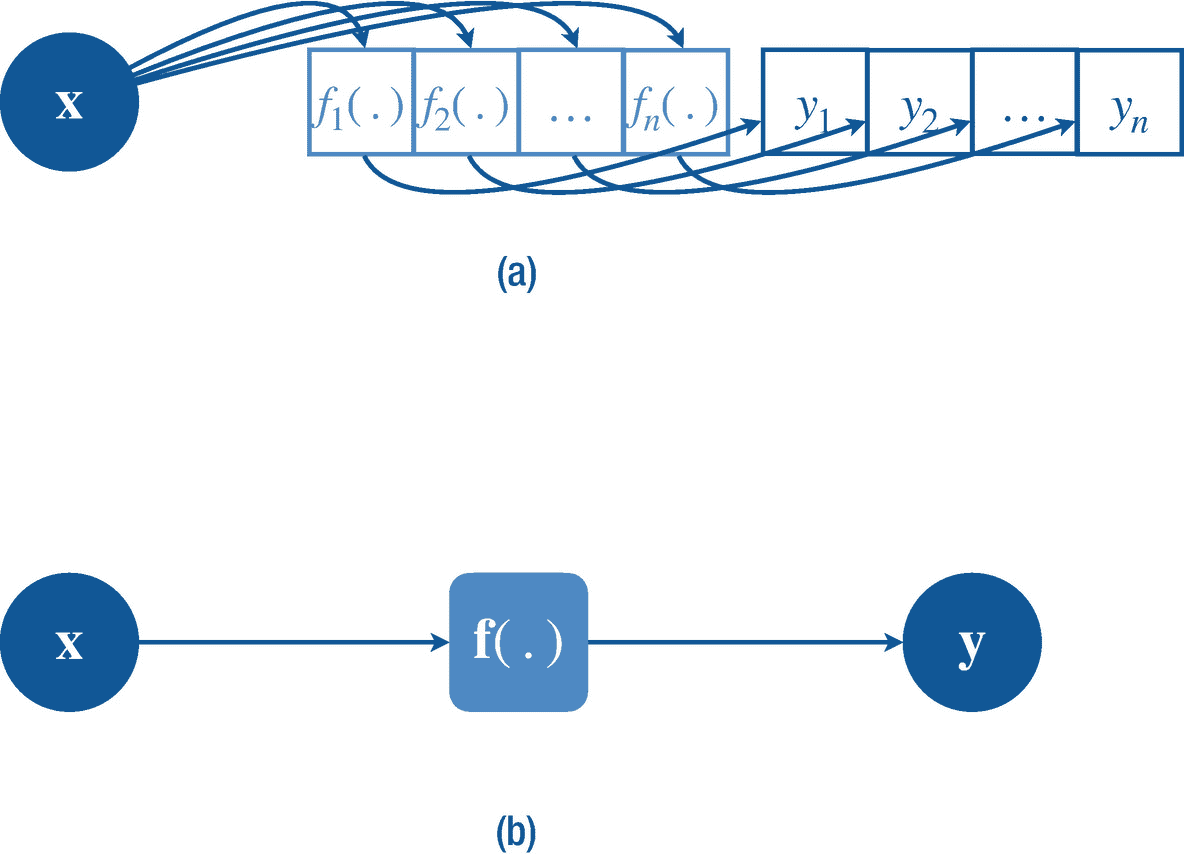
图 2-5
一个向量函数 f(。)从 x ∈ ? m 到 y ∈ ? n 的映射在(a)中明确示出,在(b)中紧凑示出
2.3.1.4 矩阵函数
我们还可以定义更高维的函数,比如一个矩阵函数,定义为从向量到矩阵的映射f:?m→?n×o或从矩阵到矩阵的映射f:?×m×n→?o 我们来看看矩阵函数中的向量到矩阵的映射,它只是一个列向量中的向量函数的集合,其中列向量中有nf=f1…fnfj:?m当 f 列 vector 中的每个向量函数应用于输入向量变量x∈?m时,它返回一个向量yj=fj(然后我们将这些输出沿着 q 行堆叠起来,创建一个矩阵y=f(x**)∈?n×o。**
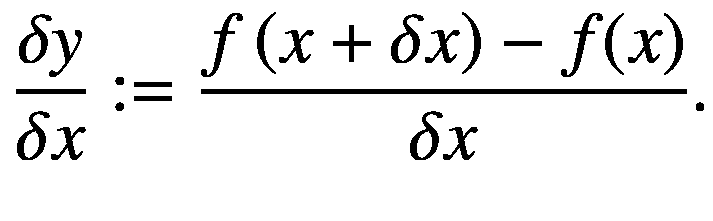
(2.46)
这里, δ 是一个希腊字母δ用来表示一个小值。在上式中,δy=f(x+δx)—f(x)是输入 δx 有微小变化时输出函数值的变化。当 δx = 0 时,则 δy = 0。该比率代表割线(将图形分成两部分或更多部分的线)的斜率,如图 2-7 所示。
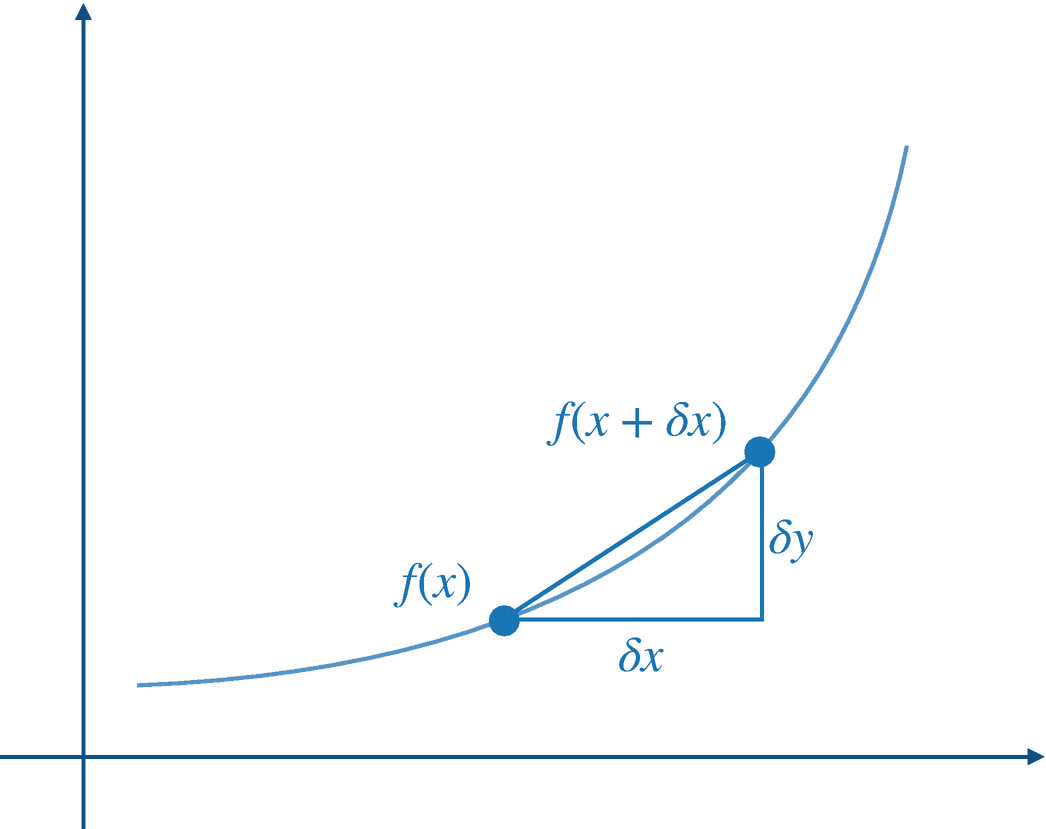
图 2-7
一元函数从(x,f(x))到(x + δx,f(x + δx))的割线
当输入值的这种明显的小变化变得可以忽略不计时,也就是说,它接近 0,表示为 δx → 0,我们得到在 x 处切线的斜率。切线是在点 x 处平行于曲线的线,代表曲线在 f ( x )处的斜率。如果函数 f (,则导数存在。)是可微的。对于一个要可微的函数,它必须在输入空间的每一点都是连续的,一个极限必须存在于微分点,并且该极限也必须存在于接近它的给定点的左边和右边。如果一个函数满足这三个要求,它就被认为是可微的。请记住,我们在神经网络文献中处理的所有函数都是可微的。函数 f 的导数(。)定义为
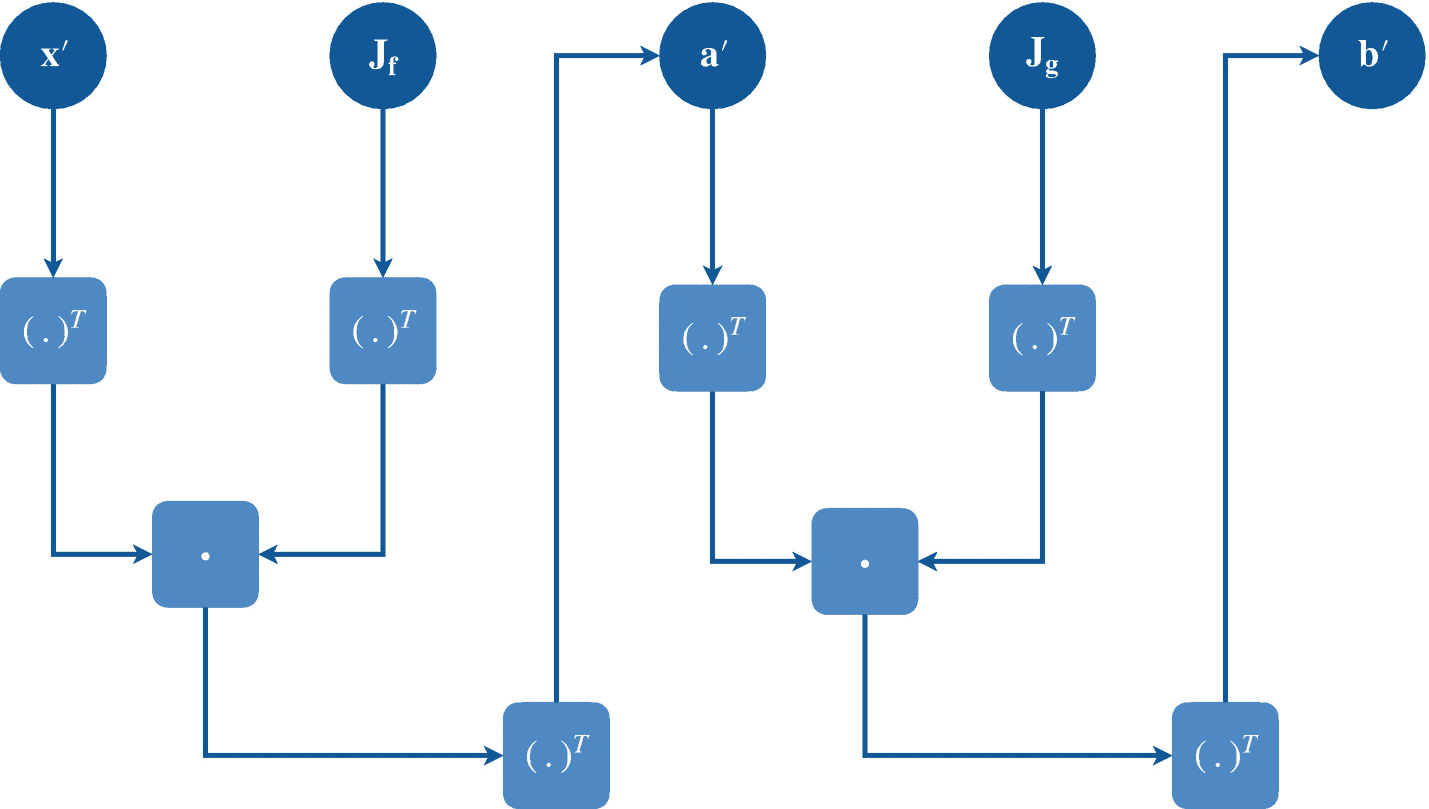
(2.47)
这里,h0,是一个非常非常小的正数。一个函数的正切 f (。)在点 x 是 f′(x)的导数,指向输出函数值最陡上升的方向。我们用 f 的导数来表示。)在 x 处为f'(x)。如果函数的输入是一个常数,那么导数就是 0,因为常数不能变化。
一些可微函数,如 sigmoid、softmax、ReLU 等,在神经网络中是如此常见,以至于我们通常宁愿记住它们的导数函数,而不是再次找到它们。这些列出的功能称为激活功能,在第 5.4 节中详细讨论。
2.3.2.1 微分法则
有时我们需要用初等算术运算来计算复合函数或多函数的导数。这里,我们遵循下面描述的四个微分规则。以下一般规则适用于单变量函数:
-
求和规则??f(x)+g(x)′=f′(x)+g′(x)
-
产品规则??f(x)g(x)′=f′(x)g(x)+f(x)
-
链式法则??f(g(x))′=f′(g(x)g′(x)
-
商法则 :
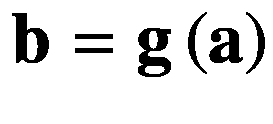
我们前面讨论过一元函数的微分。但是当我们必须处理一个多输入变量的函数,称为多元函数时,偏导数的概念就被利用了。在偏导数中,函数的导数是针对每个变量单独计算的,同时将其他变量视为常数,每个常数输入变量的偏导数为零。多元函数的偏导数 f (。)关于某输入变量 x 1 的写法如下:
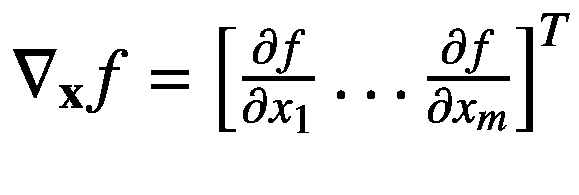
(2.48)
这里?f(x)/?x1 是 f (。)相对于x1 意味着在这个偏导数的计算过程中其他变量保持不变。这个计算函数 f 的偏导数的过程。)对行向量x∈?m中的每个输入变量重复。然后我们将这些偏导数累加到一个行向量中,称之为多元函数 f 的梯度(。)定义如下:
![$$ {
abla}_{mathbf{x}}f=frac{mathrm{d}flef<em></em>t(mathbf{x}
ight)}{mathrm{d}{x}_1}=left[begin{array}{c}{lim}_{h o 0};frac{flef<em></em>t({x}_1+h,dots, {x}_m
ight)-flef<em></em>t({x}_1
ight)}{h} {}vdots {}{lim}_{h o 0};frac{flef<em></em>t({x}_1,dots, {x}_m+h
ight)-flef<em></em>t({x}_m
ight)}{h}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402712.png)
(2.49)
因为梯度是多元函数的导数,我们可以写成 df(x)/dx,而?f(x)/?xI表示 f (。)相对于单个输入变量 x i 。有时候我们也会用 grad f (。)而不是 nabla 符号?xf来表示梯度。我们可以用更简洁的方式重写前面的等式,如下所示:
![$$ {
abla}_{mathbf{x}}f=left[begin{array}{c}frac{partial f}{partial {x}_1} {}vdots {}frac{partial f}{partial {x}_m}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402892.png)
(2.50)
后面为了方便,我们将假设梯度?xf∈?1×m为矩阵而不是向量。正如我们将在后面看到的,对于向量函数(例如,密集连接的神经网络),这个梯度的行维度大小将增加,从而它将成为一个包含向量函数偏导数的矩阵。
偏导数的 2.3.3.1 规则
通过将之前讨论的单变量函数的规则扩展如下,可以容易地获得用于计算更高维函数的偏导数的规则:
-
求和规则 :
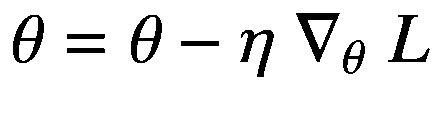
-
产品规则 :
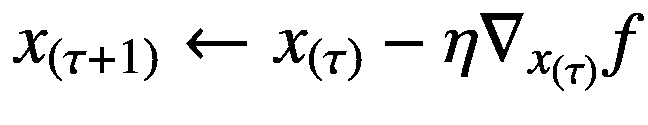
-
链式法则 :

我们已经取消了偏导数的商规则,因为在神经网络中,我们将主要处理这三个规则。请注意,这些规则类似于衍生产品的规则。请记住,函数在偏微分过程中的顺序非常重要,因为现在涉及到了矩阵和向量,并且与标量函数相比,这些数据结构上的一些操作(例如乘法)是不可交换的。
接下来,我们介绍向量函数的微分,这是训练神经网络的关键。
我们以前已经讨论过向量函数。让我们考虑一个向量函数f:?m→?n从 m 到 n 维向量空间的映射。如前所述,我们有一个包含多元函数映射的行向量f=[f1…fn】fI:?m→?.向量函数的导数可以用极限定义写成如下:
![$$ {
abla}_{mathbf{x}}mathbf{f}==left[begin{array}{ccc}{lim}_{h o 0};frac{f_1lef<em></em>t({x}_1+h,dots, {x}_n
ight)-{f}_1lef<em></em>t({x}_1
ight)}{h}& dots & {lim}_{h o 0};frac{f_{mathrm{n}}lef<em></em>t({x}_1+h,dots, {x}_n
ight)-{f}_{mathrm{n}}lef<em></em>t({x}_1
ight)}{h} {}dots & ddots & dots {}{lim}_{h o 0};frac{f_1lef<em></em>t({x}_1,dots, {x}_n+h
ight)-{f}_1lef<em></em>t({x}_n
ight)}{h}& dots & {lim}_{h o 0};frac{f_nlef<em></em>t({x}_1,dots, {x}_n+h
ight)-{f}_nlef<em></em>t({x}_n
ight)}{h}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402772.png)
(2.51)
这里将?xf∈?n×m矩阵与向量函数 f ( x )的一阶偏导数累加,称为雅可比矩阵。注意,包含矩阵的导数或其他高维函数的高维张量也称为雅可比矩阵;类似于张量,雅可比也是存储偏导数的张量的广义名称。我们可以将雅可比矩阵?xf改写如下:
![$$ {mathbf{J}}_{mathbf{f}}={
abla}_{mathbf{x}}mathbf{f}=left[begin{array}{ccc}frac{partial {f}_1lef<em></em>t(mathbf{x}
ight)}{partial {x}_1}& dots & frac{partial {f}_nlef<em></em>t(mathbf{x}
ight)}{partial {x}_1} {}dots & ddots & dots {}frac{partial {f}_1lef<em></em>t(mathbf{x}
ight)}{partial {x}_m}& dots & frac{partial {f}_nlef<em></em>t(mathbf{x}
ight)}{partial {x}_m}end{array}
ight] $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402862.png)
(2.52)
这里, J f 是函数 f ( x )的雅可比? x f 的另一种表示方式。注意每一行都是多元函数fI(x)的梯度。正如我们前面所讨论的,雅可比矩阵可以被认为是多个多元函数梯度的累加,每个函数都堆积在不同的行中,从而得到一个偏导数矩阵。换句话说,多元函数的导数是一个函数行向量中只有一个函数时雅可比的特例。
接下来,我们介绍矩阵函数的微分和一个便于计算的简单技巧。
这里,我们考虑一个简单的情况,我们计算输出矩阵变量y∈?n×o相对于输入向量变量 x ∈ ? m 其中f:?m→?n×这里我们设置 n = 3, o = 4, m = 2。这描述了一个从 m 维向量空间到 n × o 维矩阵空间的函数映射,即f:?2→?3×4。我们知道,存储输出矩阵相对于输入向量的偏导数的雅可比矩阵将是一个张量jf∈?(3×4)×2。我们演示了两种方法来计算这个雅可比。
第一种方法,如图 2-8 所示,雅可比矩阵很简单。这里我们简单计算一下 Y 相对于向量 x 的每个标量输入变量的偏导数。这些偏导数分别是?y/?x1 和?y/?x2。现在我们把所有这些偏导数整理成一个形状为(3 × 4) × 2 的雅可比张量。
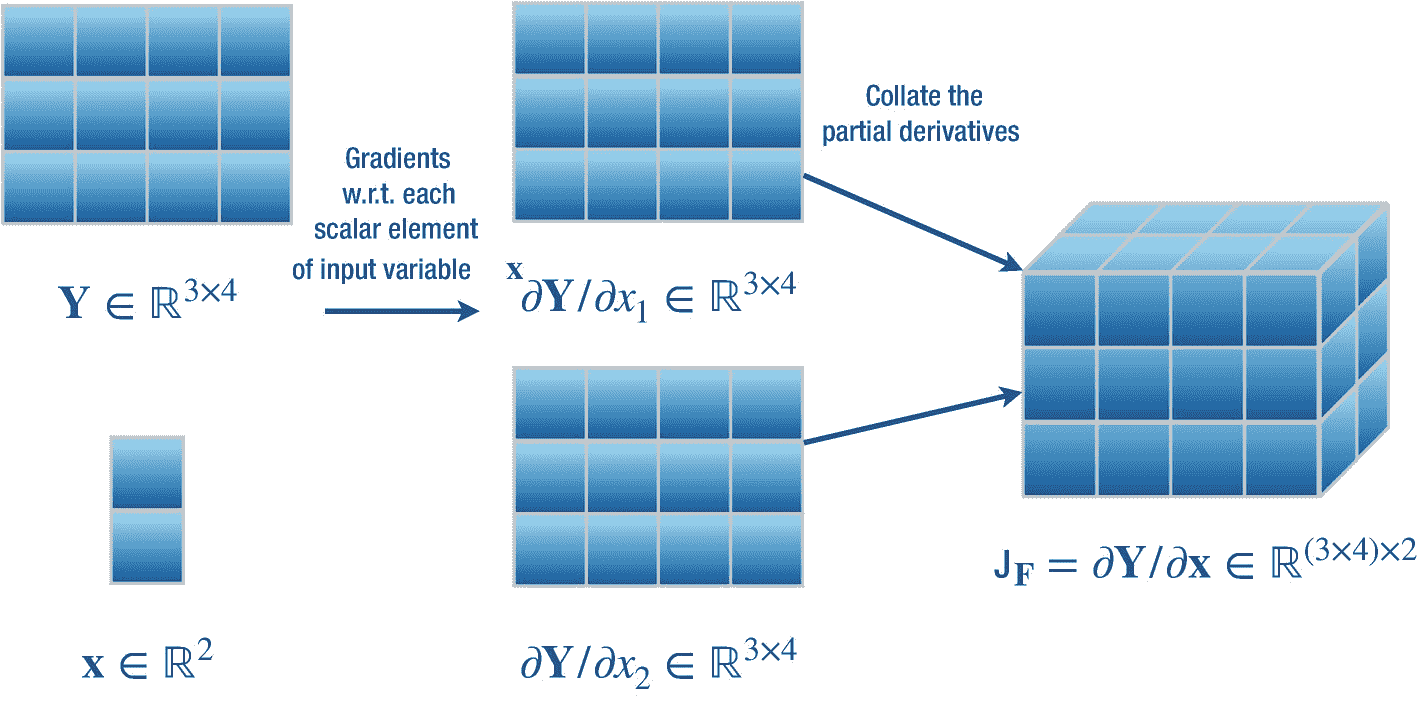
图 2-8
计算矩阵 Y ∈ ? 3×4 相对于向量 x ∈ ? 2 的梯度的简单方法
第二种方法如图 2-9 所示,雅可比矩阵的计算也很简单,但需要对之前的过程稍加修改。第一步,我们将输出矩阵展平成一个号 -或 12 维向量,即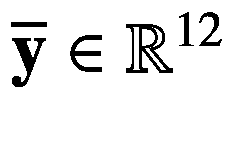 。在第二步中,我们计算这个新的输出向量 y 相对于输入向量 x 的偏导数,这导致两个偏导数?y/?x1 和?y/?x2,每个都属于? 12 向量空间。我们将这些收集在一个形状为 no × m 或 12 × 2 的雅可比矩阵中。最后,在第三步中,我们将其重塑回 a(n×o)×m—或(3 × 4) × 2 维雅可比张量,该张量现在包含输出矩阵 Y 相对于输入向量 x 的偏导数。
。在第二步中,我们计算这个新的输出向量 y 相对于输入向量 x 的偏导数,这导致两个偏导数?y/?x1 和?y/?x2,每个都属于? 12 向量空间。我们将这些收集在一个形状为 no × m 或 12 × 2 的雅可比矩阵中。最后,在第三步中,我们将其重塑回 a(n×o)×m—或(3 × 4) × 2 维雅可比张量,该张量现在包含输出矩阵 Y 相对于输入向量 x 的偏导数。
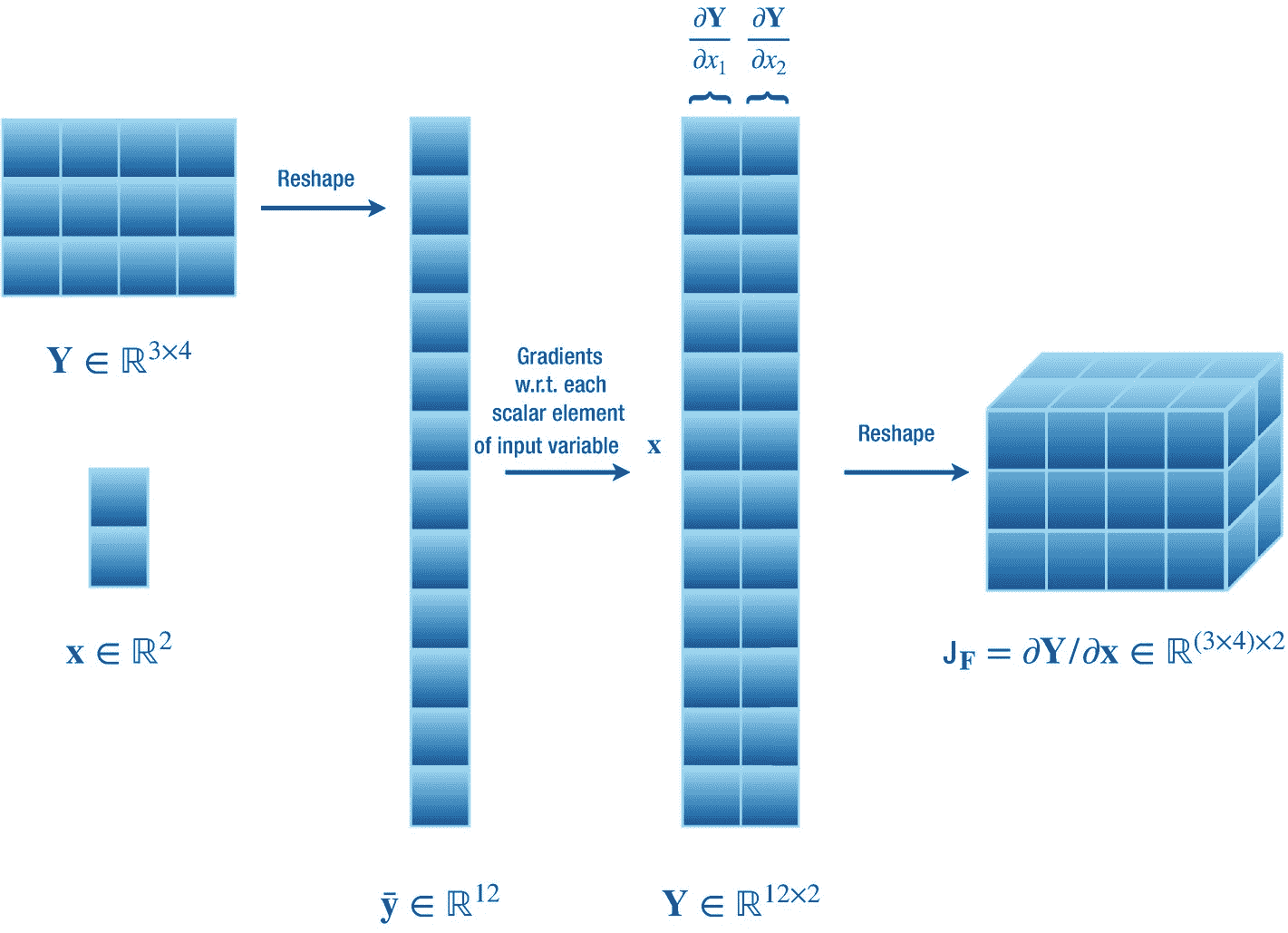
图 2-9
计算矩阵 Y ∈ ? 3×4 相对于向量 x ∈ ? 2 的梯度的另一种向量整形方法
在第四章中介绍的 Swift for TensorFlow 中的 TensorFlow 库采用了第二种方法来计算雅可比张量,这是因为第二种方法简单高效。这也使得在算法微分(第 3.3 节)中使用链式法则通过雅可比向量乘积(JVP)和向量雅可比乘积(VJP)分别在正向模式和反向模式算法微分中计算链式复合函数的偏导数变得容易。我们将在下一章描述这些术语。
请注意,第二种方法可能容易出错,因为张量的重新排序可能会破坏计算预期最终正确输出的路径,即这里的雅可比矩阵,但幸运的是它不会。为了理解这一点,我们回到线性代数来寻求一点帮助。这种方法之所以成为可能,是因为张量空间本质上是同构的,也就是说,任何空间都可以通过矩阵乘法等线性代数运算转换到另一个空间。这个变换可以再次被还原,把我们带到原始的张量空间。所以矩阵可以被改造成向量,反之亦然,同样的方法也适用于更高维的数据结构。
数学对于理解深度神经网络至关重要。在这一章中,我们讨论了三个数学分支的各种主题,即线性代数、概率论和微分学。这些都有助于设计和训练机器学习模型,我们将在后面的章节中看到。如果你在试图理解神经网络或对它们编程时迷失在更高层次的抽象中,我们建议你使用这一章作为参考。
下一章是关于用 Swift 编程语言进行微分编程。我们将广泛使用微分概念来描述算法微分,并描述 Swift 的 API 来轻松计算函数和数据类型的导数。**
Swift 是 LLVM 编译器的语法糖。
—克里斯·拉特纳
在本章中,我们首先通过比较(第 3.1 节)Swift 语言与 Python 语言的强大功能,启发您采用 Swift 语言进行深度学习。我们还引入了一种称为“TensorFlow 的 Swift”的扩展语言(3.2 节),用于通用编程以及学习和研究深度学习领域。对自动计算复合函数的导数至关重要的算法(通过从用户那里抽象出复杂性)称为算法微分,将在 3.3 节中详细介绍和讨论。然后介绍 Swift 语言的各种基本和先进的强大功能(3.4 节)。由于当前 Python 语言大量用于数值计算,我们展示了 Swift for TensorFlow 如何轻松访问(第 3.5 节)Python 的内置和库。最后,我们以总结结束本章(第 3.6 节)。
本章从“差异化编程宣言”(Wei et al .,2018)中得到很大启发,该宣言为 Swift 提供一流的差异化功能支持奠定了基础,使其成为一种更加通用的编程语言。
同时,数据科学研究团体使用的重要数字处理库(Buitinck 等人,2013;哈里斯等人,2020),机器学习(阿巴迪等人,2016;Chollet 等人,2015;Paszke et al .,2017,2019),量子计算(Aleksandrowicz et al .,2019),量子机器学习(Bergholm et al .,2018),计算神经科学(Taylor et al .,2018),其他都是用 Python 写的。虽然 Python 现在非常重要,但它不是一种好的通用编程语言(即,可用于软件开发栈的各个部分),它有许多严重的缺点,如性能慢、内存管理差、因为 GIL 而没有多线程支持、因为它是一种解释型语言而没有严肃的调试工具、高度动态的类型系统、没有对移动开发的真正支持等等。为了探索 Python 语言的替代方案,特别是机器学习,社区在不同的差异化编程研究领域对 Julia 语言进行了一些努力(Bezanson 等人,2012 年,2017 年)。但是 Julia 也有一些严重的缺点,例如不直观(如果你已经是 C++或 Python 程序员)、复杂且混乱的语法、膨胀的特性列表、怪异的变量范围、不安全且高度动态的类型系统(如 Python,允许同名变量的重新声明)、不支持移动开发等等。由于这些和其他缺点,Python 和 Julia 仍然不适合与数值计算有关的各种研究领域。
机器学习库通常用扩展的 C++语言编程,例如 CUDA (Zeller,2011),以允许在硬件加速器上执行。Python 只是与 C++代码库进行接口,使底层代码抽象,从而允许您使用简单的 Python 语法编写深度学习应用程序。因此,经过训练的机器学习模型必须加载到 C++中,以便在生产中进行低延迟部署。您的程序和低级 C++代码之间的这种差距是巨大的,它阻碍了您轻松地对特定于程序的优化代码库进行更改。Swift for TensorFlow 的目标是成为轻松编写低级优化程序所需的唯一语言,同时为您提供对高级 API 的访问,从而消除您的代码和实际机器学习代码库之间的差距。
我们知道 Swift 是一种静态类型的语言,但它也允许动态类型。例如,尽管协议(见第 3.4.6 小节)不是类型,而是一致性类型必须遵循的规则,但您仍然可以将协议用作实体的类型,该实体的实际自定义类型在运行时确定。但是 Python 没有类型的概念,除了完全动态的类。这给机器学习应用程序带来了一个问题,因为知道实例的类型反而允许编译器报告编译时错误,这使得研究人员、从业人员和学习者同样高效。这就是 Swift for TensorFlow 大放异彩的地方!但是 Python 不会检查任何错误,直到在执行过程中遇到错误。由于机器学习训练是耗时的,并且在某一语句中遇到错误(该语句直到通过某些条件才被执行)会使程序崩溃,并且训练可能需要重新开始,这使得机器学习编程非常低效。
与 Python 不同,Swift 是一种基于 LLVM 编译器的通用、快速的编译语言,并且具有通过 LLDB 调试器进行调试的本机支持。Swift 还支持自动引用计数,您几乎永远不需要担心内存管理。Python 的 GIL 有效地阻止了设备多核的使用,因此不支持多线程。但是你可以用 Swift 轻松编写多线程程序。正如已经提到的,Python 不允许应用程序开发,而现在所有运行在苹果设备上的应用程序都是用 Swift 语言编写的。
Swift 是一种开源语言,不仅能在 macOS 上完美运行,还能在 Linux 和 Windows 操作系统上运行。Swift 用于为苹果设备构建应用。Swift 在前端和服务器后端也工作得很好,分别用 SwiftUI 2 构建用户界面(UI)和用 Vapor、 3 等库处理数据库。Swift 还可以用于处理亚马逊网络服务(AWS) Lambda 运行时。 4 现在 Swift 的编译器也支持一级可微编程,这使得编写参数优化算法变得很容易。可微分编程是一种编程范例,其中使用算法微分来计算类型和函数的导数。
几乎软件堆栈的任何部分都可以在 Swift 中轻松开发。在不到十年的时间里,Swift 已经迅速成为一种通用编程语言。现在我们将看看用于 TensorFlow 语言的 Swift,它扩展了原始的 Swift 语言,以便于编写深度学习算法。基本上,Swift for TensorFlow 引入了 TensorFlow 库和 Swift 中没有的各种深度学习特定功能。
Swift for TensorFlow (S4TF)使机器学习项目的原型化变得很容易。虽然也有可能部署 S4TF 模型,但我们不会触及这个领域。由于 S4TF 具有新手和有经验的程序员友好的语法,学习曲线可以很短。S4TF 也可以作为第一语言学习编程,甚至机器学习。而且 S4TF 有很多 Python 用户会觉得有趣的强大特性。
除了在 CPU 上运行深度学习程序,S4TF 还可以在 GPU 或 TPUs 等硬件加速器上执行。在撰写本文时,S4TF 在自己的 X10 库中为 TensorFlow 使用了 XLA 编译器。这允许你在硬件加速器上执行你的算法,如 GPU 或 TPU,只需对你的代码做很小的修改,我们将在后面的章节中训练我们的机器学习算法时看到。但在未来,TensorFlow 将与 MLIR 一起构建(Lattner and Pienaar,2019;Lattner 等人,2020)编译器,其中 MLIR 代表“机器学习中间表示”MLIR 将成为机器学习库的标准。MLIR 将允许机器学习代码的设备无关的执行,也就是说,任何新的硬件加速器都将很容易得到支持。
S4TF 不仅在 Xcode 集成开发环境(IDE)中运行良好,而且在 macOS、Linux 和 Windows 操作系统的浏览器中的 Google Colaboratory 和本地 Jupyter Notebook 上也运行良好。但在 Xcode 中构建应用程序是有益的,因为它允许智能的上下文感知代码完成、高度受控的调试、断点、创建和执行测试、甚至在源代码编译之前修复程序警告和错误等等。它甚至允许您实时查看磁盘读写数据传输统计数据、发送或接收的网络数据,以及最重要的内存消耗。每年在苹果全球开发者大会(WWDC)期间,Xcode 都会不断增加新功能,以提高开发者的工作效率。这些用于开发惊人的苹果平台应用程序的 Xcode 功能也有助于开发更好的机器学习应用程序。
我原本计划用 Xcode 编写本书中呈现的所有深度学习程序,但已经在深度学习领域的许多用户在 Linux 上使用 Python,所以他们可能不会使用 macOS。为了方便他们,我使用了谷歌合作平台来构建和训练书中介绍的所有深度学习模型。因此,您可以简单地启动您最喜欢的浏览器,并立即开始尝试代码示例。你们中拥有 MAC 的人可能会在 Xcode 中执行相同的代码。
在 S4TF 中,您可以简单地导入预构建甚至安装的 Python 库,并像在 Python 程序中一样使用它们。这被称为 Python 互操作性(详细讨论见 3.5 节)。由于 Swift 的语法非常类似于 Python,调用这些函数是无缝的,感觉就像你在用 Python 编写一样。一个有趣的事实:你可以导入 Python 的任何深度学习库(例如 PyTorch)并在 S4TF 中定义和训练机器学习模型!您还可以导入 Python 的可视化库用于绘图目的。Python 互操作性有助于使用研究人员和从业者非常喜爱的 Python 库,同时仍然使用 S4TF 的其他强大功能。
在未来,iOS、iPadOS、macOS、watchOS 和 tvOS 开发人员将能够完全使用 S4TF 在纯 Swift 中编写机器学习应用程序,而不需要苹果提供的任何高级库,如 Core ML、自然语言等等。这样,你将能够灵活地编程(通过使用新的优化器、损失函数等来定义和训练新的神经层。)并在设备上分发部署了最近研究的机器学习算法的应用程序。这些设备上高度定制的模型还将维护您用户的数据隐私。希望有一天,你也能够在神经引擎上运行你的模型,以便在设备上快速处理数据。有趣的是,您已经可以使用当前的 S4TF 工具链在 Xcode 中构建 macOS 应用程序。书上写的程序都用的是 S4TF 0.11 版。
下一节将详细描述计算神经网络导数的技术。本节并非理解 Swift(3.4 节)的依赖项,但我们强调您至少要阅读一次,以便您可以在机器学习之外的其他领域高效地使用这项技术。
这里我们讨论算法微分 (AD),也叫自动微分,自动计算一个函数的导数。首先,我们讨论计算导数的各种编程方法(3.3.1 小节)。然后我们描述 AD 的两种模式(3.3.2 小节)。最后,我们展示 AD 是如何实现的(3.3.3 小节)。
注意,AD 不是专门用于机器学习,而是已经应用于各种领域,例如计算流体动力学(比朔夫等人,2007;穆勒和库斯丁,2005;托马斯等人,2010)、最优控制(瓦尔特,2007)、工程设计优化(卡萨诺瓦等人,2000;福斯和埃文斯,2002 年)。(Baydin 等人,2017 年)用更长的篇幅回顾广告。
确定函数的导数主要有四种方法,即手动求导、数值求导、符号求导和算法求导。我们简单看一下前三种区分技术。由于 Swift 使用算法区分技术实现了区分功能,我们对此进行了更深入的技术探讨。理解算法差异并不是使用差异 API 的先决条件,但是了解它可能会帮助你编写更好的差异程序。
3.3.1.1 手动、数字和符号微分
手动区分是一种非常简单但耗时的程序区分方法。过去,机器学习研究人员使用它来寻找损失函数的导数,并将其插入到优化算法中,如 L-BFGS(朱等,1994 年)或随机梯度下降(SGD)(博图,1998 年)。在这里,人们在纸笔上写下一个函数的导数表达式,然后在计算机上编写该导数函数的程序。
数值微分与导数的有限差分近似有关,在第 2.3 节详细讨论。虽然它很容易实现,但其简单性带来了一些缺点,如不准确的近似,因为值可能会由于机器精度限制(Jerrell,1997 年)而被四舍五入,并采用 O ( m )计算多元函数 f 的梯度![$$ {
abla}_{mathbf{x}}f={left[frac{partial f}{partial {x}_1}dots frac{partial f}{partial {x}_m}
ight]}^T $$](http://fmiwue.riyuangf.com/file/upload/202410/07/010402882.png) :?m→?其中 x ∈ ? * m * 是输入向量。梯度、雅可比和海森的评估时间很重要,因为深度学习算法广泛使用向量和矩阵微分。
:?m→?其中 x ∈ ? * m * 是输入向量。梯度、雅可比和海森的评估时间很重要,因为深度学习算法广泛使用向量和矩阵微分。
符号微分是计算导数的另一种方法。在符号微分中,程序操纵函数表达式以获得其导数表达式(Grabmeier 和 Kaltofen,2003)。然后,我们可以简单地用新导出的导数表达式来计算函数在某一点的导数。函数表达式到其导数表达式的转换是通过使用 2.3.2 和 2.3.3 小节中讨论的微分规则来实现的。
虽然符号微分消除了手动微分和数字微分的局限性和弱点,但导数表达式存在“表达式膨胀”的问题(Corliss,1988),这使得它们阅读和理解起来复杂而晦涩。此外,手动和符号微分阻碍了可微分程序的表达能力,因为它们不允许可微分函数包含控制流语句。为了克服这些障碍,我们求助于算法微分技术。
3.3.1.2 算法微分
算法微分是基于这样一个事实,即任何数值计算都是由一组导数已知的有限基本运算组成的(维尔马,2000;Griewank 和 Walther,2008 年)。通过应用微分的链式法则,可以计算这些函数的导数,从而获得整个表达式的导数。这些基本运算包括二元和一元算术运算以及超越函数,如对数、指数和三角函数。
AD 甚至可以区分控制流,如条件分支、循环、控制转移语句和递归。这是可能的,因为最终,任何数值程序(甚至包括控制转移语句)在执行时,将总是产生具有输入、中间和输出值的数值执行轨迹,这是使用微分链规则计算导数所需的唯一东西。
AD 可以通过两种方式实现,即正向模式和反向模式。您编写原始程序,该程序在执行时会产生一个执行跟踪(也称为正向原始/执行跟踪)。然后 AD 的正向和反向模式分别使用它生成一个相应的正向切线和一个反向伴随轨迹,这代表了数值程序的导数对应部分。生成的轨迹接受输入值并返回导数函数的输出。请注意,您使用 AD 的任何一种模式来计算数值程序的导数,而不是同时使用两种模式。
我们考虑一个多元复合函数 f ( x 1 ,x2)= sin(x1)+log2(x2),其计算图形如图 3-1 所示,我们的目标是计算下文解释了这两种方法。
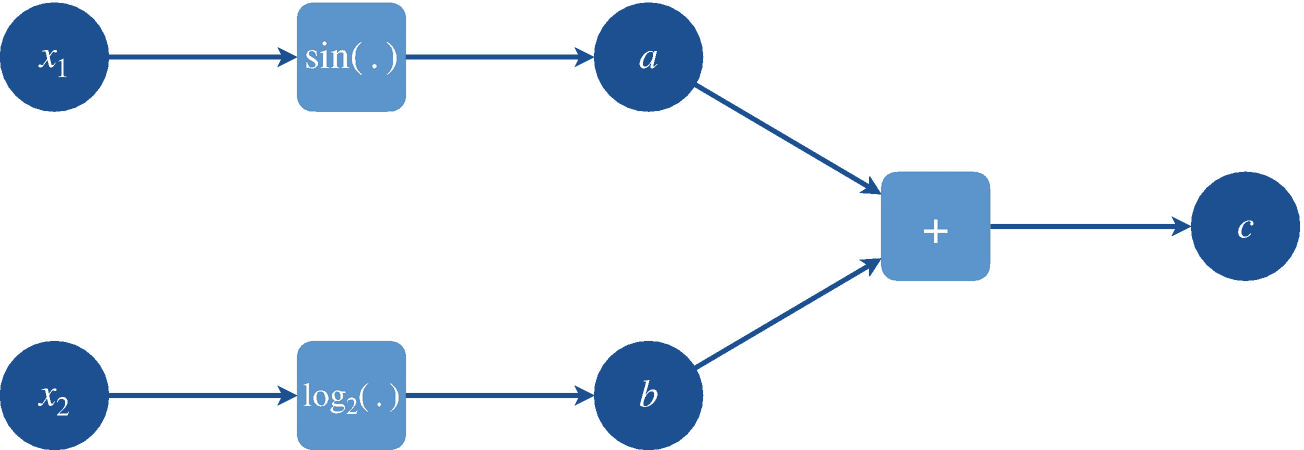
图 3-1
多元函数 f(x 1 ,x2)= sin(x1)+log2(x2)的计算图
由于 AD 要求初等函数应该是可微的,因此有导数,我们从图 3-1 所示的计算图中列出所有函数开始:
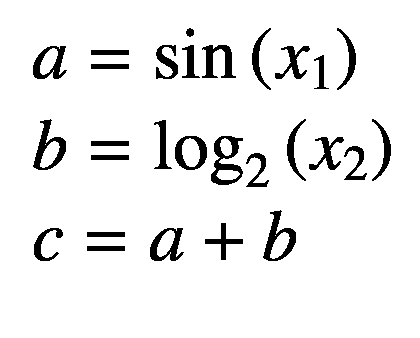
现在我们列出它们的导数如下:
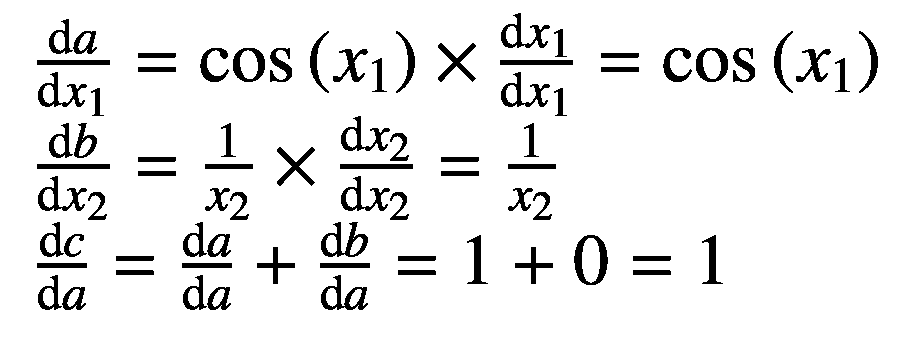
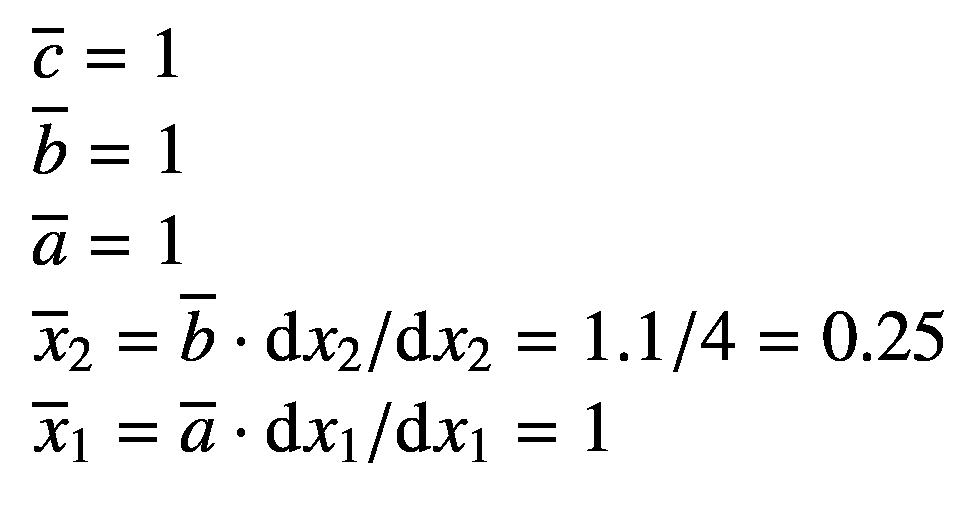

图 3-2
任意向量复合函数 g ° f(x)的计算图。
现在,我们将使用链式法则中的这些导数来寻找复合函数f(x1,x2)相对于前向和反向模式 ADs 中的每个输入变量的偏导数,如下所述。我们演示寻找偏导数?c/?x2 的正向模式以及?c/?x1 和?c/?x2 的反向模式。对于正向模式,我们用撇号表示每个变量的偏导数,例如a′=?a/?x2(也叫正切)。对于反向模式,我们用一个横杠表示每个输出变量 c 的偏导数,例如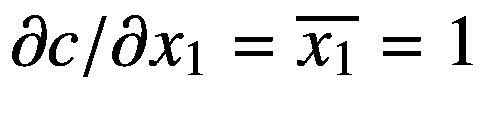 (也叫伴随)。
(也叫伴随)。
3.3.2.1 前进模式
在正向模式中,我们执行正向原始(数值程序)和正向切线追踪(数值程序的衍生物)。我们将输入值( x 1 、 x 2 )传递给函数 f ( x 1 、 x 2 )并开始跟踪正向原始程序,存储中间值 a 、 b 和 c 。通过相应的原始追踪步骤,我们也追踪相应变量的正切值。在开始追踪之前,我们将特定输入变量相对于自身的导数设置为 1,将其他变量相对于该变量的导数设置为 0。

图 3-3
任意向量复合函数 g ° f (x)的前向模式算法微分计算图。
表 3-1
前向模式算法微分的计算轨迹。
|正向原始迹线
|
正向切线迹线
|
| --- | --- |
|  |
|  |
|
请注意,链规则中使用了初等函数的现有导数,从输入变量开始,计算输出变量相对于输入变量的偏导数。这里,我们得到?c/?x2=c′= 0.25。
前向模式广告中的“前向”一词来源于这样一个事实,即我们依次计算输入变量、中间变量、然后输出变量相对于输入变量的切线。前向模式 AD 也称为前推 AD ,因为我们使用链式法则将输入变量的导数推向输出变量。
现在考虑两个任意向量函数f:?m→?n和g:?n→?o和输入向量变量x∈?1×m(我们将其表示为 a 这里我们感兴趣的是复合函数 g ° f ,如图 3-2 所示。因为这些函数由初等函数组成,类似于前面的多元函数的例子,我们已经将它们的偏导数存储在它们各自的雅可比矩阵中,即jf∈?m×n和jg∈?n×o现在,我们执行正向原始追踪,如下所示:
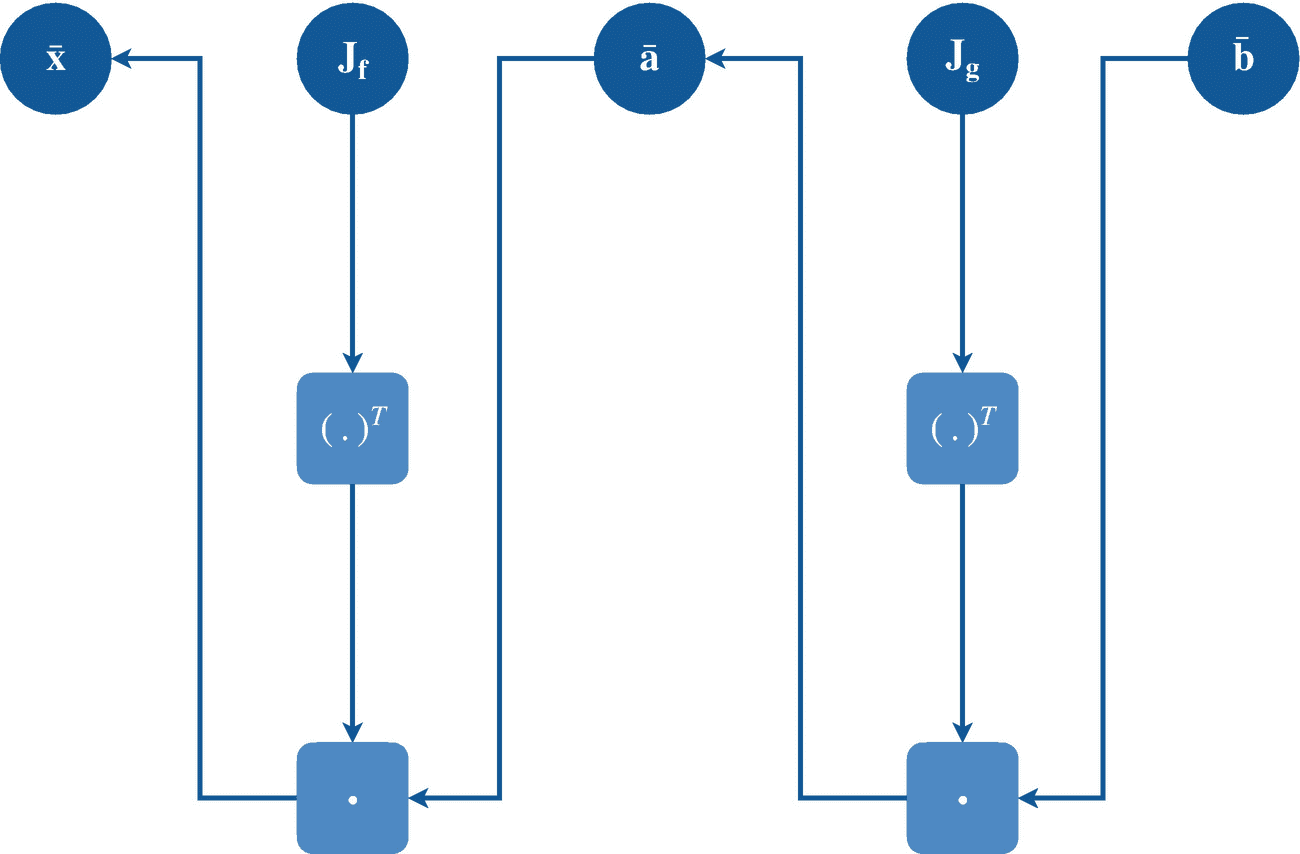
图 3-4
任意向量复合函数 g ° f (x)的逆向算法微分计算图。
这里我们有中间变量 a ∈ ? 1×n 和输出变量 b ∈ ? 1 ×o 。我们将设置 d x /d x ,这是一个 1 × m 矩阵,表示为x’,只有一个元素设置为等于 1。我们现在可以执行正向切线追踪(如图 3-3 所示)如下:
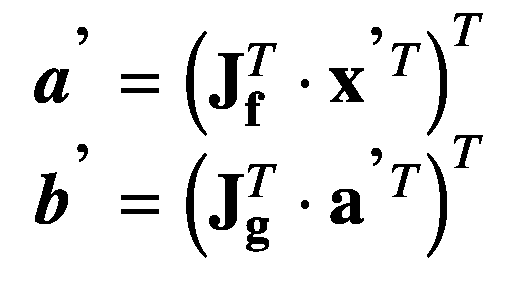
这里,我们有中间变量的导数a′∈?1×n和输出变量的导数b′∈?1×o,它们与它们的前向原始追踪变量对应项具有相同的维数。因为 we 矩阵相乘,用算子、雅可比和向量(表示为矩阵)表示,前向模式 AD 可以表示为雅可比向量乘积 (JVP)的链式应用。
当我们在点a′,即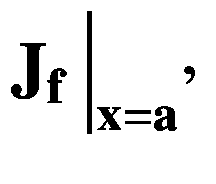 处对Jf求值时,其中a′中只有一个变量等于 1,而其余的都是零,这需要 n 个计算步骤来使用前向模式方法找到所有输出变量相对于单个输入变量的偏导数;因此,其复杂程度的顺序是 ?? ( n )。在特殊情况下,当我们有 m = 1 并且 n ≥ 1 时,雅可比矩阵可以一步计算出来。但是当nm 时,我们使用另一种技术进行快速计算,如下所述。
处对Jf求值时,其中a′中只有一个变量等于 1,而其余的都是零,这需要 n 个计算步骤来使用前向模式方法找到所有输出变量相对于单个输入变量的偏导数;因此,其复杂程度的顺序是 ?? ( n )。在特殊情况下,当我们有 m = 1 并且 n ≥ 1 时,雅可比矩阵可以一步计算出来。但是当nm 时,我们使用另一种技术进行快速计算,如下所述。
3.3.2.2 反向模式
在反向模式中,我们执行正向原始(数值程序)和反向伴随追踪(数值程序的衍生物)。与正向模式不同,在正向模式中,我们并排计算原始和切线跟踪,反向模式 AD 是一个两步过程。这里,我们首先执行正向原始追踪,然后在第二步中执行反向伴随追踪。第一步,也称为正向传递,我们将输入值( x 1 , x 2 )传递给函数f(x1, x 2 )并开始跟踪正向原始程序,存储中间值 a ,第二步,也称为向后传递,我们从输出变量开始向输入变量追踪变量的伴随值。在开始跟踪之前,我们将标量输出变量相对于自身的导数设置为 1。
表 3-2
反向模式算法微分的计算轨迹
|正向原始迹线
|
反向伴随迹
|
| --- | --- |
| 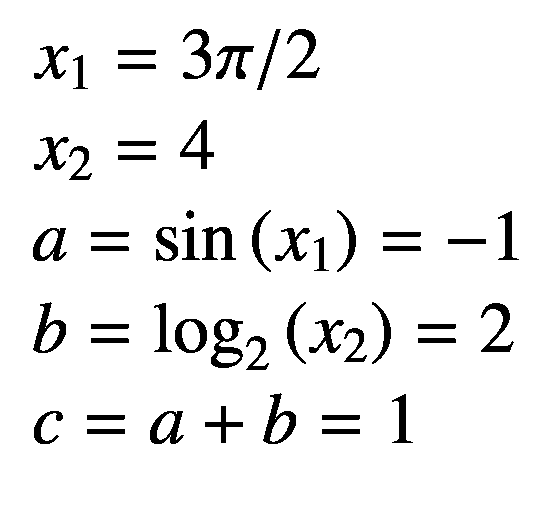 |
| 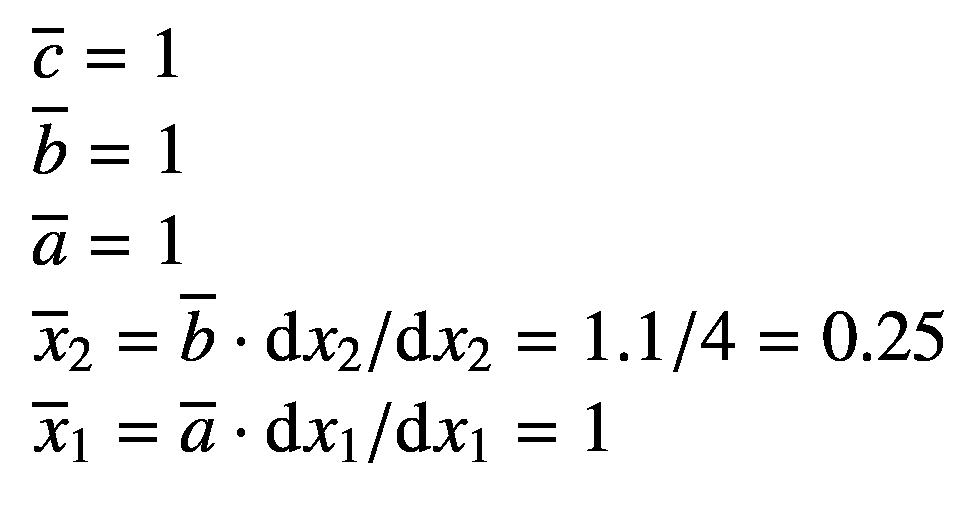 |
|
在这里,我们得到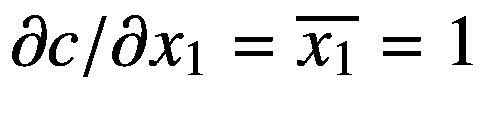 和
和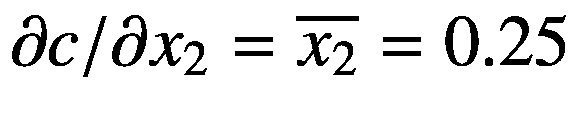 。
。
反向模式 AD 中的“反向”一词来源于我们依次计算输出变量相对于输出变量、中间变量、然后是输入变量的偏导数。反向模式 AD 也称为拉回 AD ,因为我们使用链式法则将输出变量的导数拉向输入变量。
从前面的前向模式 AD 讨论中,我们考虑关于向量函数 f 和 g 及其雅可比矩阵 J f 和 J g 的相同假设。然后我们执行正向原始追踪(如图 3-4 所示),如下所示:
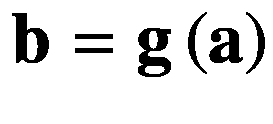
这里,我们又有了中间变量 a ∈ ? 1× n 和输出变量 b ∈ ? 1× o 。我们将设置 d b /d b ,它是一个 1 × o 矩阵,表示为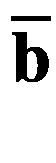 ,只有一个元素设置为等于 1。我们现在可以如下执行反向伴随追踪:
,只有一个元素设置为等于 1。我们现在可以如下执行反向伴随追踪:
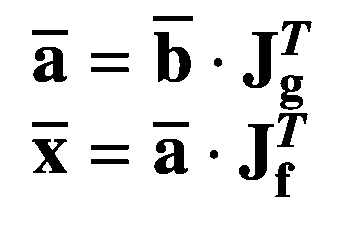
这里,我们有关于中间变量 和输入变量
和输入变量 的输出导数,它们与它们的前向原始追踪变量对应变量具有相同的维数。因为我们将向量和雅可比矩阵相乘,所以反向模式 AD 可以表示为向量-雅可比乘积 (VJP)的链式应用。
的输出导数,它们与它们的前向原始追踪变量对应变量具有相同的维数。因为我们将向量和雅可比矩阵相乘,所以反向模式 AD 可以表示为向量-雅可比乘积 (VJP)的链式应用。
当我们在点 评估 J ** g ** 时,即
评估 J ** g ** 时,即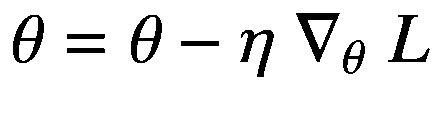 处,其中
处,其中 中只有一个变量等于 1,其余的都是零,这需要 m 个计算步骤,以使用逆向模式方法找到所有输出变量相对于所有中间和输入变量的偏导数;所以它的复杂程度顺序是 ?? ( m )。在特殊情况下,当我们有 m = 1 并且 n ≥ 1 时,雅可比矩阵可以一步计算出来。
中只有一个变量等于 1,其余的都是零,这需要 m 个计算步骤,以使用逆向模式方法找到所有输出变量相对于所有中间和输入变量的偏导数;所以它的复杂程度顺序是 ?? ( m )。在特殊情况下,当我们有 m = 1 并且 n ≥ 1 时,雅可比矩阵可以一步计算出来。
当我们在下一章研究神经网络时,我们将看到神经网络的梯度计算总是这种特殊情况,因为损失函数发出标量值。这就是为什么今天的深度学习库只实现反向模式 AD 的主要原因(尽管 Swift 实现了正向和反向模式,这使它成为一种更通用的语言,可以应用于除深度学习之外的其他各种领域),因为输出标量相对于所有中间和输入变量的梯度可以在一次反向传递中计算出来。在本书中,我们还关注使用 Swift 的反向模式 AD 功能(第 3.4.9 小节)。
这里我们讨论两种实现 AD 的方法,即操作符重载(OO)和源代码转换(SCT)。
3.3.3.1 运算符重载
通过为数字自定义类型定义高级操作符(参见 3.4.8 小节),也称为操作符重载(OO),可以很容易地实现算法差异。一些 Python 库如 autograded(Maclaurin 等人,2015;Maclaurin,2016)、5py torch(Paszke et Al .,2017,2019)、6python IC tensor flow(Abadi et Al .,2016)、7Keras(Chollet et Al .,2015)、8Theano(Al-Rfou et Al .,2016)、这些被称为嵌入式(他们的宿主语言是 Python) 特定领域语言(DSL),因为它们解决了特定领域的问题(这里是深度学习),并且作为库分发。
清单 3-1 中的代码给出了一个简单的例子(改编自(Wei et al .,2018))使用双数实现 Swift 前向模式算法微分的运算符重载,用于计算给定表达式的导数。
输出
我们声明了一个包含两个存储属性的结构,这两个属性是符合协议的类型的和。然后扩展到包括各种高级运算符,如加、减、乘、除。每个函数都返回一个包含和的实例。这里,加法和减法、乘法和除法分别使用和、积和商的微分规则来初始化要返回的实例的属性。
然后我们用 3 的和 1 的初始化文字。这里设置等于 1 意味着相对于自身的导数等于 1。我们声明了计算x3+x的文字,其相对于的导数为 3 x 2 + 1。当我们访问属性时,我们得到了 3 * 3 2 + 1 = 28。
注意,任何 DSL 的局限性在于,它受限于只能实现 AD 的一种模式,即正向或反向模式。但是编译器级别的代码转换,如 Swift 语言,让我们实现这两者。
3.3.3.2 源代码转换
实现 AD 的一个更好的方法是执行程序的编译器级源代码转换(SCT ),这允许在语言本身中实现正向和反向模式!程序员可以简单地调用 API 来区分使用正向或反向模式的函数。SCT 在编译过程中为在编译器级别执行优化提供了更多的控制,以实现快速区分。
一个 SCT 优化示例如下。在数值执行跟踪期间,考虑一个条件语句(在每个条件传递中包含不同的数值计算)。在正向正切或反向伴随跟踪期间,DSL 将需要跟踪这些条件中的每一个,以形成计算图来优化程序执行性能。如果有 c 条条件语句,那么就需要运行跟踪 c 次;现在,如果您还考虑控制转移语句,那么将需要更多的跟踪。相比之下,编译器级 SCT 可以考虑 Swift 的每个特性,并在编译过程中优化所有可能的情况。这将只需要跟踪一次来累积变量值,并且偏导数将被快速计算。
SCT 正是 Swift 解决上述技术缺点的方法。尽管讨论 SCT 超出了本书的范围,但我们确实讨论了 Swift 中可用的各种差异化 API(第 3.4.9 小节)。但在此之前,让我们在接下来的章节中熟悉一下 Swift 语言本身。
在本节中,我们将通过 Swift 语言的足够多的功能来理解书中的机器学习程序。熟悉 Python 或 C++的有经验的程序员会发现 Swift 语法很容易掌握。对于初级程序员来说,Swift 代码感觉像是在读英文句子,因此代码语句背后的意图变得直观易懂。除了简单的语法之外,Swift 还是一种快速、跨平台、编译和类型安全的语言,具有诸如泛型、回溯建模、协议、可选等现代特性。涵盖 Swift 的所有特性超出了本书的范围。苹果在线提供的神奇 Swift 图书 10 将对对 Swift 其他功能感兴趣的读者很有帮助。
我们从简单的值开始(第 3.4.1 小节),然后看看如何在 Swift 中使用各种集合类型(第 3.4.2 小节)。3.4.3 小节介绍了控制流语句。第 3.4.4 节讨论了 Swift 中的三种功能形式。然后我们引入自定义类型(3.4.5 小节)。第 3.4.6 小节讨论了 Swift 的一些强大而现代的功能。第 3.4.7 小节展示了如何轻松处理 Swift 中的错误。3.4.8 小节介绍了类型的自定义运算符。最后,我们在第 3.4.9 小节中介绍了 Swift 的算法差异化功能,以此结束本节。
在 Swift 中,您分别使用关键字或将实例声明为变量或常量。您可以在程序执行期间更改变量实例的值,而常量实例的值不能更改。
遵循 Swift 约定,您应该用小写字母 camel 声明一个实例。
这里,被推断为类型。前面代码中声明的常量被推断为类型,因为它包含十进制值。在某些情况下,您可能需要声明一个浮点数。在这种情况下,只需提供作为变量的类型信息。您还可以使用功能验证每个实例的类型。
输出
类型信息是从分配给实例的值中自动推断出来的。在其他情况下,您可以通过编写类型名称,后跟由冒号分隔的实例来提供类型信息。
这是一个很好的例子,表明在 Swift 中阅读代码语句就像阅读英语句子一样。Swift 简单的语法让新手学习编程变得很容易。
在某些情况下,实例可能不包含值。为了表示实例的这种状态,Swift 提供了可选值,这些值要么包含一个值,要么不包含任何由表示的值。若要定义可选的,请在声明期间提供类型信息,后跟一个问号(?)不带任何空格。
输出
这里,是值为 5 的类型。它本来可以包含,因为它是可选的。然后,语句提取并绑定常量中的值,供语句的代码块使用。这叫做可选绑定。
您还可以定义 computed 属性,该属性计算值而不是存储值。计算的属性必须始终声明为变量实例。参见清单 3-24 中的示例。
您可以在 Swift 中声明三种集合,即数组、集合和字典。集合是一种通用结构,在无法推断类型信息的情况下,您必须为其提供类型信息。每个集合类型都符合协议,该协议允许您迭代它的元素。
3.4.2.1 阵列
数组是元素的有序集合。你访问一个元素,它的下标代表它在数组中的位置。在 Swift 中,数组是零索引的,也就是说,数组的第一个元素的位置是零,第二个元素的位置是一,依此类推。
输出
还可以用实例方法访问每个元素的索引位置。清单 3-6 中的代码对数组进行排序和枚举。
输出
3.4.2.2 集
集合是唯一元素的无序集合。在声明中,指定实例属于类型。您可以执行数学集合运算。集合也有一些类似于标准库中数组的方法。
输出
偶数和奇数是整数的子集
您可以定义一个集合,该集合的类型后跟一个尖括号中的类型信息,例如,因为是一个通用结构类型。但是如果信息可用,您可以省略类型信息。尽管集合是无序的,但是您可以使用实例方法对它们进行排序。注意这里三元运算符的用法写为。如果条件为真,则返回,否则返回。在这里,偶数和奇数的并集是整数的子集,这是一个 true 语句,因此返回。
3.4.2.3 词典
字典是无序元素的集合,其中每个元素都是一个键和值对。通过在实例中使用键作为下标来访问值。
输出
注意,我们在访问人力车的轮数时使用感叹号。返回一个可选值,因为字典中可能不存在某个键。使用感叹号来访问可选值被称为强制展开。请注意,这可能会失败,所以在您不确定字典中是否存在键的情况下,请尝试使用可选绑定,如下所示。
输出
前面代码中使用的条件语句是下面讨论的许多其他控制流的一部分。
Swift 提供各种控制流语句。您可以使用三种循环来遍历一系列语句。条件语句允许您根据条件的真实性执行特定的语句。还可以使用控制转移语句将执行控制转移给某些语句。
3.4.3.1 环线
Swift 有三种循环,分别是循环、循环、循环。每一个都有其重要性,如下所述。
循环允许您迭代地访问集合实例中的每个元素。您还可以在迭代期间通过调用集合上的实例方法来访问每个元素的索引。
输出
这个例子简单地在从 1 到 5 的范围内迭代。您可以使用语法排除范围中的最后一个数字(5)。
输出
将函数与符合的两个实例一起使用,可以在相应的索引位置访问每个实例中的元素。这里,和分别处于和的零位。运行循环在第一次迭代中访问这两个文件,并打印“苹果有红色。”类似地,为每个对应的元素对打印其他句子。
循环适用于在一个范围或的一致性实例上迭代的情况。但是当迭代次数未知时,while 循环会很有帮助。While 循环只是在条件为真时运行一段代码,否则终止。while 循环有两种,即循环和循环。
循环在开始时检查条件,并重复一组语句,直到条件变为假。相反,除了不需要条件检查的第一遍以外,当所有遍的条件都为真时,循环执行一组语句。
输出
这里,循环在开始时检查的值是否大于零。如果该条件为真,则执行花括号中的语句。但是当的值变得等于或小于零时,循环终止,将控制返回到右花括号后的代码,如果有的话。
输出
在前面的循环中,花括号之间的一组语句在第一次循环中执行。它首先用终止字符而不是(回车符,将光标移动到换行符)打印出的值,然后通过给加 1 来更新它的值。最后,如果的值超过 6,它就中断循环。这是循环终止条件。运行这些语句一次后,检查条件是否大于零,以再次执行循环。注意循环可能无限执行一系列语句,您必须提供一个终止条件,就像我们在前面的代码中提供的那样(循环内部)。
3.4.3.2 条件语句
Swift 支持两种条件语句,即和。
在语句中,如果条件为真,则执行一段代码。此外,如果您的条件为假,您可以定义一个要执行的代码块。如果您想检查一个以上的成功条件,您还可以在和代码块之间提供一个语句,因为它不能在一个语句中用逗号分隔。
输出
这个例子展示了如何将条件语句与和语句结合起来,对代码执行进行细粒度控制。因为在 60 和 80 的范围内,所以这段代码打印“平均值”
另一个有用的条件语句是。语句用于比较单个实例和多个可能的值。
输出
这里,语句将单个变量与许多可能的情况进行比较。注意如何使用或关键字定义一个局部变量或常量,并在那里比较它的值。您还可以检查位于特定区间的值。在语句中,充当语句中的块。如果你的陈述不够详尽,就必须包括在内。当任何第一次遇到的情况被匹配并且其代码被执行时,程序的控制被转移到语句的右花括号之后的代码行。但是如果您想执行后续的 case 代码,而不管它是否与值匹配,您可以使用控制转移语句。如果这个例子中没有包含,那么它将只打印“Average”语句模仿 C 和 C++语言中条件语句的行为。
3.4.3.3 控制转移报表
Swift 提供了五种控制转移语句,即、、、和。下面的错误处理中讨论了语句。和已经在前面的文本中讨论过。语句与语句一样用于函数中。您也已经看到了清单 3-13 中的语句的例子。
这里,我们重点关注循环中使用的控制转移语句。
输出
在这段代码中,函数产生一系列值,从 0 到 40,间隔 10,不包括最后一个值,即 50。通过转换为数组来打印范围,显示它所描述的值。要包含最后一个值,在这个函数中用替换参数。然后 循环遍历所有的值,打印每个值,但不是 30。这是通过使用一个语句完成的,该语句将执行控制转移到下一次迭代的 循环的第一条语句,跳过所有后续语句。
3.4.3.4 提前退出
在语句中,关键字后面的代码如果是条件就必须为真,或者如果是可选的就必须包含一个值,以便执行语句后面的代码。在可选绑定的情况下,实例在出现语句的代码中是可用的,以供进一步使用。但是如果失败,那么执行代码块中的代码。这个块还必须包含一些控制转移语句,将控制转移到编写语句的代码块之外。
输出
这里,函数以一个字典作为参数。然后,语句试图从字典中提取键的值。如果字典中没有键,可选绑定可能会失败。在这种情况下,代码块被执行,它简单地向控制台打印一条消息。但是当该值存在时,它被存储在一个名称常量中,该常量用于打印更精细的消息。这个例子使用了一个函数特性,这将在下面详细讨论。
在 Swift 中,闭包是功能的代码块,可以在程序的不同部分重用。说得更清楚一点,Swift 提供了三种闭包,function 是其中之一:
-
全局函数是命名闭包,可以通过用它们的名字显式引用它们来调用。
-
嵌套函数是在另一个函数中声明的命名闭包。
-
闭包表达式是一个未命名的功能块,无论在哪里声明,它都会被隐式执行。
调用一个函数意味着通过引用该函数的名称来执行写在该函数内部的代码语句。
3.4.4.1 全球职能
定义一个全局函数,用关键字后跟名字,圆括号中的参数列表,花括号中的函数体包含函数的功能。
输出
前面的函数接受一个枚举类型的车辆参数(稍后讨论),表示两辆车辆。基于值,它返回一个字符串,代表它在驾驶时发出的声音。最后,我们打印出。
在 Swift 中,每个函数都是一个引用类型。Swift 中只有类和函数是引用类型。这里,是类型的函数。你可以理解为“名为的函数接受一个类型的参数值并返回一个值。”使用功能打印该功能的类型,确认该功能的类型。
3.4.4.2 嵌套函数
嵌套函数是在另一个函数内部声明的函数。
输出
的类型是,它不接受任何参数,返回一个类型的函数。嵌套函数的类型为,返回 0。在返回前面的之前,调用只会在外部函数中打印一条语句。中的变量是,当被调用时,在其中打印一条语句并返回 0,然后存储在中。
3.4.4.3 闭包表达式
闭包表达式是简单但功能强大的无名函数代码块。闭包写在一组左花括号和右花括号内。Closure 就像一个命名函数一样接受圆括号中的参数,并表示右箭头后面的返回类型。闭包的主体写在关键字之后。稍后,我们将经常使用闭包表达式来计算损失函数相对于神经网络的梯度。
输出
这里,闭包有类型,也就是说,它接受一个并返回一个。跟在关键字后面的主体计算操作并返回结果。这个闭包向实例返回一个函数,稍后调用这个函数来检查-5 是否为正数,并正确地打印出它不是正数。
输出
函数接受一个数字和一个表示该数字第二个属性的闭包。将数字 2 和函数传递给会返回 true,表示 2 是一个正整数。数组在清单 3-31 中声明。
当闭包是函数的最后一个参数时,为了简单起见,可以去掉它的参数标签和函数调用的圆括号,只在开始和结束的花括号中写闭包。这被称为尾随闭包。为了给提供一个自定义闭包,我们只需编写一个闭包,它返回一个布尔值,表明斐波那契数列中存在一个数字。在我们的例子中,2 是偶数,也包含在斐波那契数列中,所以它返回 true。
闭包要强大得多,解释它们的所有特性超出了本书的范围。例如,Swift 还有多个尾随闭包,允许你写多个闭包作为函数参数的尾随闭包。我们建议您参考在线提供的 Swift 官方书籍,以深入了解 closures 和许多其他功能。
您还可以在 Swift 中声明称为自定义类型的新类型。它可以是任何枚举、结构和类类型。枚举和结构是值类型(复制实例),类是引用类型(只引用实例,不复制实例)。每种类型在不同的情况下都很有用。
遵循命名惯例,您应使用大写字母 camel 来声明类型,以便与 Swift 标准库中已定义的其他类型保持一致。
3.4.5.1 枚举
枚举允许您定义一组彼此具有相似关系的类型。例如,您可以定义一个包含一组颜色案例的枚举。请注意,这些颜色是它们右边的类型。使用关键字来定义您的枚举。
清单 3-22 声明一个枚举并根据一个实例打印一条语句
Rainbow.violet

输出

我们已经声明了一个名为的枚举,它包含了彩虹中自然出现的所有主色。的值是用关键字声明的,它们本身就是独立的值。
通过将实例的值设置为类型为的来声明实例。然后,通过对照不同的颜色检查的值,打印出合适的语句。注意这里是如何使用点语法的。编译器自动理解在每个案例中被比较的值是类型的,所以使用点语法就足够了。
3.4.5.2 结构
结构是程序的基本构造块,它可以包含属性、方法和下标,以便为类型添加功能。结构也可以符合协议并扩展更多的特性。我们将在整本书中广泛使用结构。
清单 3-23 中的结构代码片段声明了一个结构和一个名为的嵌套枚举类型。有两个属性,分别是和。这里,是一个可选的整数实例,因为一些哺乳动物可能没有腿,而另一些可能在它们的一生中失去了腿。是描述哺乳动物生存环境的实例。
我们已经声明了三个名为、和的实例,每个实例都用不同的实例属性值初始化。你可以把的例子理解为“人类生活在陆地上,有两条腿。”同样,可以描述为“受伤的人也生活在陆地上,但失去了双腿。”最后,您可以将实例理解为“鱼生活在水下,生存不需要腿。”
输出
前面的代码扩展了结构,以包含一个哺乳动物实例的精选描述。看看如何在计算实例属性中修改实例属性,以包含基于实例属性的细化信息。最终打印出来的句子对每个实例进行了有意义的描述。注意如何扩展结构,即使在声明实例之后,仍然允许那些实例使用扩展的功能;这适用于 Swift 中的所有自定义类型。
也可以将类型实例作为函数调用。在我们的例子中,这种函数编程方法使得在神经网络中执行前向传递变得很方便。您可以通过在自定义类型中声明一个带有任意数量参数的来实现。我们将在后面章节描述神经网络模型的结构中声明这个函数。
但是有时您可能需要做的不仅仅是创建带有属性、下标和方法的实例。您可能需要从其他类型继承功能,重写某些功能,等等。类在您的类型中提供这样的功能,如下所述。
3.4.5.3 班级
就像结构一样,类也是程序的基本构建块,它可以包含属性、方法和下标,以便为类型添加功能。与结构类似,类也可以符合协议,并可以扩展更多的特性。
除了与结构共享功能之外,类还允许您从其他类继承属性、方法和下标,重写它们,进行类型转换以检查实例的类,取消实例的初始化,以及允许对类实例的多个引用。但是本书并没有讨论所有的特性。我们只浏览对理解书中的深度学习程序很重要的功能。
输出
前面的代码声明了一个包含两个存储属性和一个计算属性的基类。基于名称和火箭在太空中施加的推力,生成描述。我们声明两个实例并打印它们的描述。
注意,如果存储的属性不包含初始值,类不会自动获得初始化器(以关键字开始的代码块)的实现,初始化器必须由您提供。
输出
一些火箭比另一些更强大,可以携带更大的有效载荷。这些火箭除了普通火箭的特点之外,还有一个有效载荷的特点。使用这个想法,前面的代码继承了来自的特性,并提供了一个额外的存储属性。我们还修改了来更详细地描述。你必须在这里用关键字标记描述。注意到那个关键词了吗?这意味着这个类不允许被任何其他类进一步继承。
我们创建了的两个实例,即和。每一个都有不同的能力,我们在初始化器中提供了细节。然后通过访问 computed 属性将详细信息正确地输出到控制台。
Swift 还具有现代编程能力,即扩展、协议、泛型和差异化。有了扩展,您可以提供甚至无法访问源代码的类型的实现。协议允许您为一个类型定义一组标准(需求)。实现一个协议的所有需求的类型被称为符合该协议。Swift 提供泛型,使您的代码可用于多种可能的场景。在编译器中构建的对微分的一流支持,让您可以构建可微分的程序,从计算流体动力学(Kutz,2017 年)到机器人手运动(Akkaya 等人,2019 年),以及深度强化学习。区别特征在第 3.4.9 小节中讨论。
3.4.6.1 扩展公司
扩展允许您通过提供新功能的实现来扩展类型的功能。也可以在 Swift 中做追溯建模。换句话说,您可以扩展甚至无法访问源代码的任何类型,例如,Swift 的标准库类型,如 Array 和 Tensor(在 TensorFlow 库中可用),甚至可以扩展其他库中声明的类型,如 Foundation、Vision 等。
输出
前面的例子扩展了以包含一个实例方法,该方法通过将自身提升到方法调用期间给定的某个值来改变实例的值。该方法被标记为,因为在标准库中被声明为一个结构,而结构是值类型,与引用类型的类不同,它们不能修改自身。我们首先写一个断言,确保不是负数。然后,如果为零,则条件将实例的值设置为等于 1。稍后,一个 循环迭代地计算实例提升到的值。最后,一旦计算完成,实例被设置为等于。
扩展能够提供计算属性、方法、下标、初始化器、嵌套类型的实现,甚至使类型符合协议等等。
在第六章中,我们将看到如何扩展 TensorFlow 的协议,通过与 Python 语言的互操作来定义自定义的检查点写入和读取实例方法。这将展示我们可以利用这些现代而强大的功能侵入 Swift。
3.4.6.2 议定书
大多数程序员通常都熟悉面向对象编程。相比之下,Swift 从诞生之日起就被设计成一种面向协议的语言。因为 Swift 也是面向对象的,我们首先从协议声明开始,然后在合适的场景下使其他类型如枚举、结构和类符合它们。
这里,有三个要求,分别是类型的可获取、类型的可获取可设置和类型的可获取可设置。它要求一致性类型提供它们的实现。结构通过提供需求的实现来采用。
您还可以扩展协议来提供实现,而不仅仅是需求信息。这样,符合该协议的类型会自动获得那些实现。
输出
现在,符合的任何类型,包括以前的实现,都可以访问属性。注意,如果函数体、闭包、计算属性或返回某个值的下标中只有一个语句,我们可以去掉 return 关键字。
3.4.6.3 仿制药
泛型允许您编写单个代码块,并使用许多不同的可能数据类型执行它。这是被称为多态性的面向对象编程的基本原则之一。Swift 语法使得实现和使用通用代码块变得非常容易。在 Swift 中,您可以定义属性、下标、函数、方法甚至枚举、结构和类的泛型。
输出
Swift 已经提供了函数来交换任意两个相同类型实例的值。但是为了熟悉泛型编程,我们在前面的代码中实现了自己的版本,名为。
这里,是一个类型占位符,其类型在使用该函数之前是未知的。当您在函数调用中提供变量时,编译器会推断出该类型。关键字允许您修改函数体中的参数值,并将这些修改写回外部变量。函数调用中变量前的&符号()清楚地告诉你,它们的值在函数体内是可变的。请注意,您应该始终用关键字声明这些实例,否则它们将不会变异。您可以将函数声明理解为“声明一个名为的通用函数,带有类型占位符,并带有两个变量和
我们已经成功地交换了两个字符串的值,甚至我们自己的结构实例!您可以交换任意两个变量实例的值,只要它们属于同一类型。接下来,我们使用两个泛型类型来描述泛型的更复杂的用法。
输出
前面的有两个通用类型和,它们都符合协议。子句后的语句声明序列的每个元素必须符合(必须相等),并且和应该具有相同类型的元素。该函数将分别符合和的和作为参数,返回类型为的元素数组。最后,调用该函数只是查找并返回一组唯一的和常见的元素。
输出
这个通用函数适用于任何序列实例,并且其元素可以相等。对于实例也是如此,因为它是一个由组成的数组。
输出
就像泛型函数一样,我们也可以在 Swift 中声明泛型类型,使该类型在各种不同的场景中可重用。这里,结构被声明为一个泛型类型,有两个泛型类型和。这两个存储的属性属于不同的泛型类型。两个实例和分别用泛型类型和声明。这可以通过打印它们的类型信息来确认。
泛型不仅仅限于结构,还适用于枚举和类。它们可以被视为在 Swift 中实施多态性的一种非常强大的方式。
Swift 的另一个现代而强大的功能是差异化,这将在第 3.4.9 小节中详细讨论。
错误处理是在容易出错的情况下使程序更加健壮的一种方式。有了错误处理,您可以将程序从崩溃中拯救出来,并通过将错误信息打印到控制台来更清楚地了解错误。Swift 的简单语法有助于使错误处理代码更易于阅读和理解。
在 Swift 中处理错误的一种便捷方法是使用代码块。
输出
要表示错误,只需让您的自定义类型(这里是)符合协议。它是一个空协议,仅用于表示错误。枚举类型非常适合 Swift 中的错误表示。
只有函数会抛出错误。在参数列表后面写关键字,告诉编译器这个函数可以抛出错误。并在可能抛出错误的函数调用前编写关键字。最后,当错误发生时,使用关键字抛出一个错误,后跟错误,例如 。
前面的代码显示了如何在 ping 某个网站失败时抛出错误。可能的错误在枚举中被写成案例。对块中的函数的调用需要一个用于 ping 的链接。如果在查验时出现错误,则在块中抛出一个适当的错误。您应该考虑操作参数标签值,看看为每个值打印了什么错误消息。
这里需要注意的一件有趣的事情是在字符串中使用双引号时使用的散列符号(#)。在字符串双引号之前和之后使用 hash 可以让您在字符串本身内部写双引号。插值的一个附加变化是在反斜杠()和左圆括号之间使用了散列符号。
Swift 支持在有意义的语法中使用函数轻松实现类型上的自定义运算符。清单 3-35 是添加两个结构实例的简单例子。
输出
当你定义自己的结构时,编译器不知道任何数学运算对它意味着什么。在这里,您可以为特定的运算符定义自己的运算,例如,为加号运算符定义加法,如前面的代码所示。这个加号(+)实例方法在添加两个参数的每个元素后返回实例。该操作只是添加了两个实例,这可以通过前面的描述来验证。
通常深度学习中的领域特定语言(DSL)像 python NIC tensor flow(Abadi 等人,2016),PyTorch (Paszke 等人,2017,2019),autograd (Maclaurin 等人,2015;Maclaurin,2016),以及许多其他人在 C++代码库中使用该功能来实现张量运算和自动微分(通常是反向模式)。相比之下,Swift 采取了一种激进的方法来解决这个问题,即在编译器中实施自动微分,以获得最佳性能,并允许静态编译的语言功能和 Swift 的优势。
Swift 为算法差异化功能提供一流的支持。区分已经在编译器内部被烘焙,使得 Swift 的类型系统是可区分的。令人惊奇的是,你不必限制你的程序的表达能力,你可以自由地编写控制流语句、循环和递归,程序仍然是可微分的!您用清单 3-36 中的语句导入 _ Differentiation 库。
注意库名前面的下划线吗?这意味着该库尚未准备好用于生产(但很快就会准备好),因此不能用于在 Xcode 中构建应用程序以供分发。但是您可以在 Swift 中使用这个特性来学习、练习和研究差异化编程(甚至深度学习,我们将在后面看到)!如果你是一名应用程序开发人员,那么,在未来,你将能够开发并向你的用户分发不同编程的应用程序。
一旦导入了库,您就可以访问所有可用的差异化 API。下面的代码清单期望这个 import 语句在顶部。不可能在一本书中涵盖编程的每个细节。我们建议您参考(魏等,2018)。
3.4.9.1 可微类型
严格地说,只有函数可以微分,因此可以有导数或偏导数。更具体地说,如果一个函数的参数和结果值都是可微的,那么这个函数就是可微的。从程序上来说,这意味着参数和结果类型必须是可微的,因为函数体内部的计算也是可微的。并且这些类型不仅限于 Swift 的类型系统中由或类型表示的标量实数。但是它们也可以扩展到任何维度的向量、矩阵或张量数据结构。Swift 使得区分这种定制类型和功能成为可能。
在撰写本文时,Swift 提供了用协议声明可区分定制类型的语法上最有意义、数学上最合理的方式。
关于 Swift 的类型系统,一个有趣的事实是,诸如、、、、、等类型是在 Swift 的标准库中定义的,而不是在 Swift 的编译器中定义的。这允许增加数值计算的类型,并将它们作为语言的一等公民对待。
有不同的数学分支允许对各种类型的参数和结果进行函数微分:
-
初等微积分:数学的一个分支,我们简单地计算函数标量结果相对于输入标量的导数。
-
向量微积分:数学的一个分支,涉及向量场作为参数/结果的微分。这个分支进一步延伸到矩阵和张量领域。
-
微分几何:数学的一个分支,其中函数在流形上微分。流形是高维空间中的连通区域,其中彼此靠近的点似乎在欧几里得空间中。
接下来,我们介绍允许自定义类型执行区分的通用协议。该协议也共同满足了上述数学子领域的要求。
3.4.9.2 可区分协议
遵循 Swift 的面向协议的编程范式,为了符合不同分支中区分的数学理论,Swift 在协议中引入了可区分类型的概念。从数学上来说,能够表示实数的类型(如或)是可微的,而其他的则不是(如或)。当您尝试区分一个不可区分的类型时,Swift 编译器会发出一条人类可读的错误消息。例如,清单 3-37 中的代码无法区分。
这段代码没有编译并报告一个错误:“函数不可微。”尽管输入和返回类型都是可微分的,但函数内部的计算却不是。这是因为该值被转换成,然后再转换回,这使得计算不可微,并且不能表示实数。每当您的代码中出现此类错误时,Swift 将通过警告或错误信息(在这种情况下)引导您对代码进行修改,尤其是在 Xcode 中。这样 Swift 对于机器学习的初学者理解微分和机器学习本身是非常有帮助的。
任何符合协议的类型都可以作为参数传递给一个可微分函数,并从该函数返回。这意味着我们可以在纯 Swift 中计算函数结果相对于其参数的导数或偏导数(即,不像许多 Python 库那样使用 C 或 C++代码)。注意,对于一个可微的函数来说,函数体内部的计算也必须是可微的(参见清单 3-37 )。
Swift 已经为其基本类型(如、、、等)提供了一致性。)到其标准库中的协议。但是这种一致性不仅限于基本类型,还扩展到用户定义的自定义类型(例如,TensorFlow 库中的自定义类型),它可以包含实例和类型属性(存储的和计算的)、下标和方法。(避免声明枚举类型,因为它们不能有存储属性。)如果有某种类型目前不符合协议,您可以简单地扩展它,编译器将通过代码生成自动综合所有差异化的特定需求,这将在下面讨论。
让我们编码一个名为(改编自清单 3-35 )的三维向量,并使其可微。
sum: 4.0
??sum: Point3D(x: 0.0, y: 1.0, z: 0.0)
输出
使用回溯建模,我们首先声明名为的可微分计算属性。对声明属性的简单使用使得计算出的属性是可区分的。然后我们简单地将的梯度设为 5,并将其结果存储在常量中。数学上,dx3/dx= 3xx2在 x = 5 处计算得出 75,因此我们的代码也给出了预期的结果。
这就是 Swift 的基本特征。接下来,我们继续讨论 S4TF 特有的特性,这些特性使它成为机器学习的强大语言。第四章专门介绍 TensorFlow 和相关库中的机器学习特定功能。下一节将展示 S4TF 如何与 Python 语言进行互操作,以及如何轻松访问它的内置和自定义函数。
3.4.9.4 差异化原料药
差异化 API 遵循一种命名模式。让我们通过考虑一些例子来解释如何阅读这些闭包。首先,参数标签、、分别以变量、闭包、闭包为输入。在这里,可以读作“计算闭合在一点的梯度,并返回梯度值。”函数读起来也很简单,“计算闭包的梯度并返回它”,可以在一个期望值上求值。前缀返回包含和、或其他闭包的命名元组。
下面列出了 Swift 中的各种正向模式差异闭包。但我们不讨论这些,因为它们仍处于开发和实验阶段:
-
和
-
和
我们主要关注书中的反模式算法微分函数,讨论如下:
-
和:它们计算闭包的标量输出相对于输入标量变量(即单变量或多变量)的偏导数,并返回一个闭包。这个闭包以输出相对于自身的导数作为自变量,即 d y /d y 其中 y 是输出变量。我们通常设置 d y /d y = 1。在回调评估期间,该值在链式规则中被乘以 dy/dx= dy/dy?dy/dx,其中 x 是返回的闭包的输入变量。
-
和:基于和;因此,它们的工作方式与它们相同,但总是设置 d y /d y = 1,并简单地返回评估的梯度,而不是闭包。
-
和:这些也是基于和;因此,它们的工作方式和它们一样,但是返回一个渐变闭包,当在某个点求值时,它返回一个闭包求值的元组和值。
我们已经在清单 3-37 、 3-38 和 3-39 中展示了我们后来感兴趣的一些差异闭包。现在我们演示如何定义函数的自定义导数。
3.4.9.5 定制衍生品
我们知道立方函数f(x)=x3的导数是f'(x)= 3x2。但是如果我们想定制这个函数的导数呢?Swift 允许我们使用函数声明属性在反向模式微分中定义函数的自定义导数,而用于正向模式微分,但它仍在开发中。让我们定义所需的自定义导数。
输出
我们声明了一个返回参数的立方的函数,并初始化了一个等于 4 的常数。然后使用函数,我们计算闭包在点的导数。
接下来,我们声明了一个函数,并对其应用了属性,这告诉编译器根据该函数返回的闭包声明来计算闭包的导数。该函数返回一个命名的元组,其中分别包含类型为和的和。在的函数体内,我们将返回为,将返回为闭包。这里,代表 d y /d y ,如果传递给 variants,其值为 1,但如果传递给 variants,其值实际上取决于你。现在,当我们在计算闭包的梯度时,我们成功地获得了 8 作为输出。
我们还可以用函数声明属性定义前向模式微分的自定义导数;但是,不幸的是,在撰写本文时,它还处于试验和开发阶段。
3.4.9.6 停止导数传播
你也可以阻止导数通过整个计算图的子图传播。Swift 提供了两个闭包,即和,用于停止计算导数。在这里,参数接受一个在某个点上计算的数学表达式,它不会参与整个表达式的导数计算,而只是返回它本身的值。参数接受一个不需要计算其导数的闭包,它通过在给定点计算闭包内部的数学表达式来返回值。
输出
此示例中的所有表达式的值都是 5。在这里,的闭包表达式计算x3,计算后返回 125。但是它的导数是 3x2 应该返回 75,但是因为不涉及导数,所以我们得到(x??)'?(x+10)= 2x?(x+10),计算后得到 50。
的闭包表达式演示了一个更复杂的计算x2?(x+10),计算后返回 375。当它的导数 3x2+20x求值为 5 时,我们应该得到 175,但我们没有。这是因为子表达式 x + 10 从不参与导数计算,实际的导数在这里是 2 x ? ( x + 10),当值为 5 时返回 150。
停止梯度计算在训练各种神经网络中起着重要作用。例如,生成对手网络包含两个不同的连接的神经网络,也就是说,它们作为单个神经网络,但是它们应该被单独训练,尽管它们一起作为整个单个计算图。为了停止计算网络参数的导数,我们可以将执行计算的闭包传递给函数的参数。一些著名的重要深度学习任务,如图像风格化、对立示例生成和其他任务,也需要停止通过子计算图的梯度传播。
这就是 Swift 的基本特征。下一节将展示 Swift 如何轻松地与 Python 语言进行互操作,并轻松访问其内置和自定义功能以及任何已安装的库。
我们知道 Python 是目前机器学习非常重要的语言。如果您已经是一名 Python 程序员,您可能知道有许多重要而有用的库是用 Python 编写的。我们可能仍然希望使用这些库来保持我们的生产力。因此,无需在 Swift 中重写所有这些库,您可以直接在 Swift 中轻松地与 Python 的内置函数和安装在您系统上的所有 Python 库进行互操作。
在内部,当 S4TF 访问 Python 实体时,就会调用 Python 解释器来执行这个过程并将数据返回给 S4TF。所以 Python 操作的执行时间取决于 Python 的解释器而不是 S4TF 的编译器。为了使与 Python 动态特性的交互成为可能,S4TF 引入了结构,它可以存储 Python 解释器返回的任何数据。S4TF 中任何从 Python 导入的 Python 库、类、实例或任何其他实体都用表示。这样你也可以在 S4TF 中对执行操作,我们将在下面看到。请注意,S4TF 中可用的 Python 库可以通过包含一个带有代码的包而在 Swift 中可用。包(网址:“ ”,。Xcode 中 Package.swift 文件中的 branch("master "))。
本节假设清单 3-42 中的 import 语句被写在本节中每个代码清单的顶部。
清单 3-43 中的代码展示了一个简单的例子,演示如何在 S4TF 中使用 Python 的 NumPy 库。
输出
我们首先导入 Python 的 NumPy 库。然后我们声明并初始化两个 NumPy 数组和。最后,我们印刷他们的产品。注意在 S4TF 中使用简单的乘法运算符(星号)直接将 Python 对象相乘是多么容易。这是因为实现了这样的高级运算符。
注意,Swift 和 Python 中都存在一些全局函数和关键字,如、等。由于我们将要编写的程序是在 S4TF 中,这使得编译器很难理解我们希望编译器调用哪个全局函数。因此,为了防止这种不必要的情况在实践中出现,S4TF 为 Python 实体添加了一个名称空间,在 Python 和 S4TF 的全局函数之间添加了一个分离层,从而使 S4TF 编译器完全清楚应该调用哪种语言的全局函数。参见清单 3-44 中 Python 名称空间如何有效分离这两种语言的全局函数的例子。
输出
在前面的代码中,我们将文字初始化为。然后我们可以在 Python 名称空间中使用 Swift 的函数和 Python 的方法。值得注意的是,尽管 Swift 没有任何名称空间的概念,但这种行为可以通过使用类型方法和枚举来实现。
如前所述,Python 是一种动态类型语言,其中每种类型都继承自基类。在某个时候,你声明的变量可能包含一个值,而在另一个瞬间,它可以存储一个值,甚至任何其他用户定义的类。Python 中也没有类型安全检查。但是 S4TF 是一种可以静态和动态执行的强类型语言。S4TF 的动态操作能力让我们能够以动态的方式与 Python 进行互操作,而不会损害 Python 的动态特性。即使在 S4TF 中,这也是用户期望的最基本的 Pythonic 需求。S4TF 没有直接提供 Python 的基本类型,而是提供了对类型的访问,该类型充当 S4TF 和 Python 的基本类型之间的隔离。你可以简单地在 S4TF 中声明一个类型的变量,它的行为和 Python 变量一样,也就是说,它的值可以在不同的类型之间进行操作(比如、等)。).除了在这样的实例上调用方法,我们还可以直接在这些 Python 实例上执行算术运算。
注意,这些操作实际上是由 Python 解释器执行的,但是的操作符是在 S4TF 中声明的。参见清单 3-45 中关于 s 的操作示例
输出
我们声明并初始化两个变量和,分别有 30 和 6 个值。虽然这些是 s,但是我们可以对它们进行加、乘、减、除等各种运算。这里,我们将除以。
因为互操作性让我们可以直接从 S4TF 与 Python 对象进行交互,所以我们还可以在这些语言之间执行类型转换!要将 S4TF 类型转换为 Python 的对应类型,只需用类型对 S4TF 实例进行类型转换。如果您需要执行 Python 到 S4TF 类型的转换,您将使用您想要的 S4TF 类型对进行类型转换。但是这个类型转换在 S4TF 中返回一个可选类型,也就是,因为这个转换可能会失败。例如,当您将 Python 的对象类型转换为 Swift 的类型时,这种转换是不可能的,并且会返回一个。
毫无疑问,这个特性在某些情况下非常有用,特别是机器学习,当我们必须用 NumPy 的对象的值初始化 S4TF 的实例时,因为我们可能需要通过某个硬件加速器上的神经网络实例传递这些值,这几乎总是这样。清单 3-46 描述了这些语言之间的简单类型转换。
输出
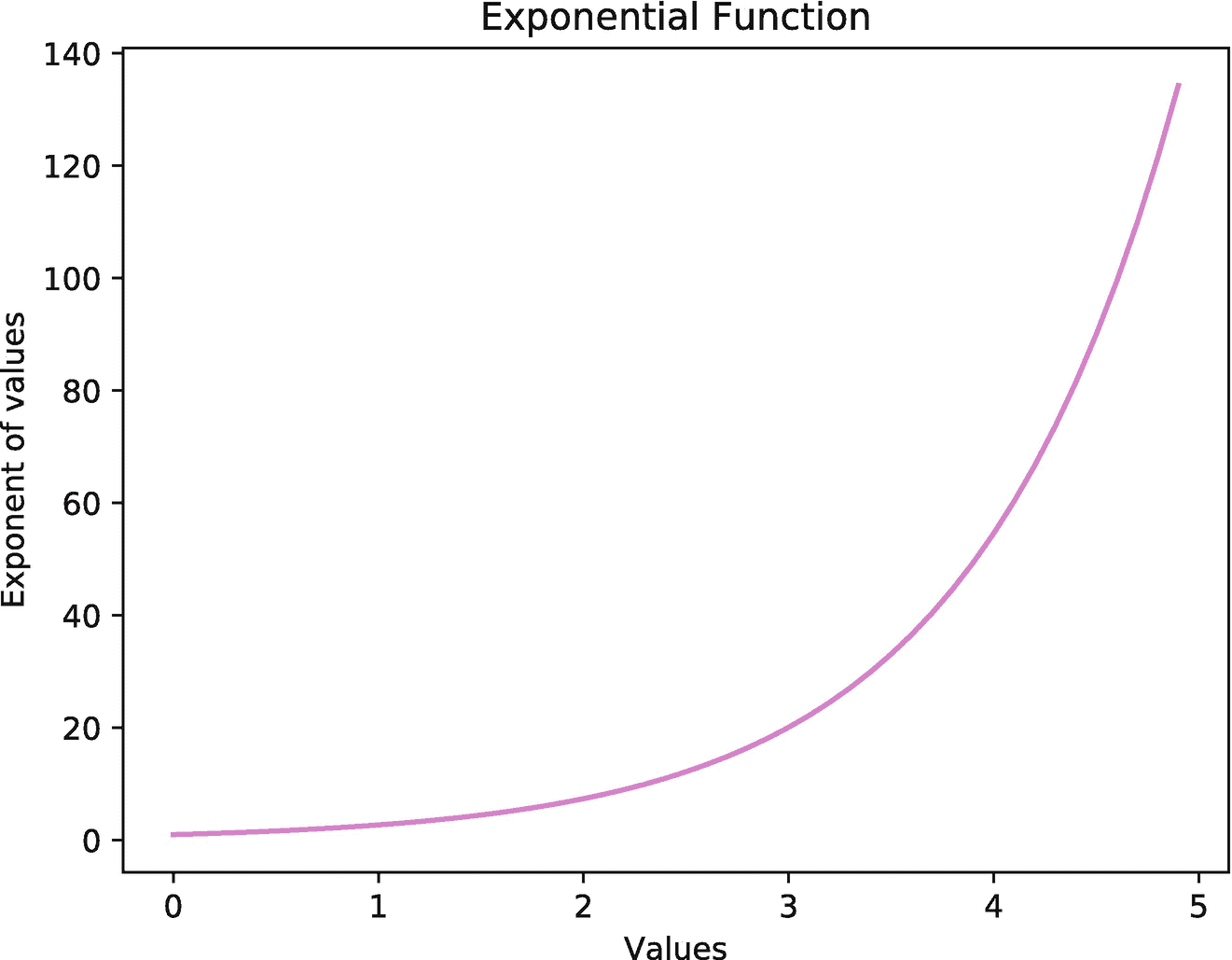
数据科学家工具箱中最重要的工具之一是可视化,即使是机器学习研究人员和实践者也需要它。借助 Python 的互操作性,我们可以很容易地在 S4TF 中进行数据可视化。简单的例子见清单 3-47 。确保您已经通过 Pip 包管理器安装了 Matplotlib 库;否则,只需在终端中运行以下命令:。

图 3-5
通过与 S4TF 的互操作,使用 Python 的 Matplotlib 库绘制的指数函数图
运行前面的代码会显示一个图像(见图 3-5 )显示范围为[0,5]的指数函数的曲线图。这里,Matplotlib 库的模块执行和变量的绘制。
Python 互操作性帮助我们在 S4TF 中使用 Python 众所周知的强大库。这为深度学习的当前 Python 用户轻松过渡到 S4TF 消除了障碍。
本章重点介绍了 Swift 语言的编程。Swift 引入了具有编译器级实施的差异化编程,而 Swift for TensorFlow 语言是 Swift 实施深度学习特定功能的扩展。本章从激励当前的深度学习社区(使用 Python)采用 Swift 语言开始。接下来,我们介绍了在 Swift 中实现的算法差异特性的具体细节。然后提供了 Swift 语言的快速浏览,使您能够轻松理解 Swift 的各种基本功能和强大功能。最后,我们介绍了 Python 互操作性特性,该特性使 Swift for TensorFlow 的用户可以直接从 Swift for TensorFlow 使用他们喜爱的 Python 库。
现在我们已经准备好理解 TensorFlow 的基础知识(将在下一章介绍),这将允许我们对深度学习进行编程。
现在最重要的事情不再是争论 Swift 是否应该存在差异化编程(因为 Swift + ML 太重要了!),而是搞清楚应该在语言中落地的最佳形式!
—理查德·魏在推特上
这一简短的实用章节旨在介绍 Swift for TensorFlow 的一些深度学习特定功能。第 4.1 节介绍了张量数据结构的概念,它实质上是神经网络进行预测的基础。阅读本章后,你将能够加载数据集(第 4.2 节),编写自己的神经网络(第 4.3 节),训练你的模型并测试其准确性(第 4.4 节)。除了所有这些,在 4.5 节,你还将学习如何实现你自己的新层,激活函数,损失函数,和优化器。这将有助于原型化您的研究代码或实现深度学习算法的高级构建模块。本章要求对机器学习有所了解。我们建议您通过阅读第一章来更新您的概念。
在第二章中,我们已经学习了标量、向量和矩阵的概念以及一些重要的运算。这里,我们将它们形象化以帮助我们理解,并引入张量的概念来概括它们。理解张量很重要,因为构成本书主题的神经网络本质上是操纵张量值来进行预测的。
张量是一种可以在 n 维空间中存储数值的数据结构,其中 n ≥ 0。有一些常见的张量如标量、向量和矩阵,它们的维数(称为秩)分别是零、一和二。当我们需要存储秩大于 2 的高维值时,我们使用术语张量。换句话说,张量概括了前面提到的所有低维数据结构。
TensorFlow 提供了用于初始化任意维度张量的类型。它提供了两个重要的实例计算属性,即和。属性返回一个代表实例维数的值。例如,vector 实例的为 1。属性返回一个代表每个维度中元素数量的值。比如一个包含三行两列的矩阵,有[4,3]的(程序化),数学上我们写成[4 × 3]。清单 4-1 展示了一些的例子,这些例子在图 4-1 中可以看到。
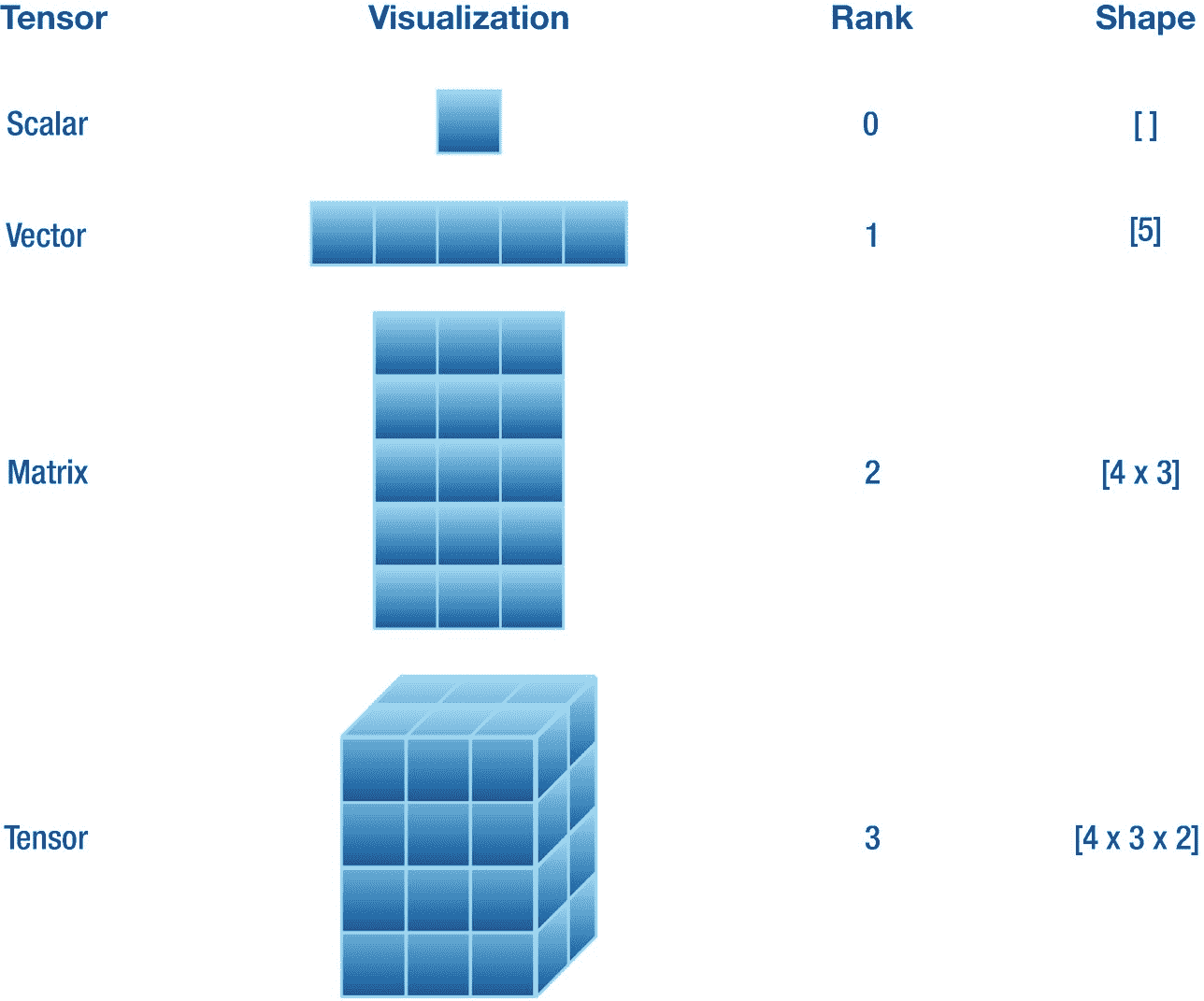
图 4-1
各种张量及其相应的秩和形状属性的可视化。在这里,每个方块包含一些数值
输出
请注意,是一个泛型类型,需要我们为占位符类型传递类型。占位符类型的类型是在初始化期间在尖括号中提供的,尖括号允许我们在那个实例中存储指定类型的元素。例如,清单 4-1 中声明的所有张量对于都有一个类型。注意是符合协议的的类型占位符,因为符合那个协议,我们可以将设置为类型。
在清单 4-1 中,我们声明了不同等级和形状的各种张量,然后打印出来用于演示。注意,类型有各种各样的初始化器可以灵活初始化。我们声明、、和为的实例。实例的为 0,而为[ ]。实例的为 1,而为[5]。实例有 2 的和【4,3】的,即四行三列。实例有 3 的和[4,3,2]的。所有这些情况都可以在图 4-1 中看到。
接下来,我们讨论 TensorFlow 中的数据集加载。
在撰写本文时,TensorFlow 允许加载图像和文本域中的各种数据集。但是我们会关注图像数据集。在加载这些数据集之前,您需要在 Xcode Swift 包的 Package.swift 文件中添加 swift-models 包,如下所示,或者您可以在 Xcode 项目设置中添加包 URL:
如果你正在使用谷歌实验室,那么在你的 Jupyter 笔记本的顶部写下以下声明:
这将加载 tensorflow/swift-models 存储库,并仅构建数据集库。但是如果你想建立其他的库,比如 TrainingLoop 和 Checkpoints,那么就把它们写在 Datasets 被写的地方,但是用一个空格分开。现在,我们可以导入数据集库,如下所示:
在整本书中,我们隐含地假设这个 import 语句是在我们加载任何数据集的地方编写的。现在让我们看一下与数据加载相关的一些概念。
有两个与数据集采样相关的主要概念,即时期和小批量(或简称为批量)。
批次是一组单独的数据样本,其中批次大小定义了该批次中样本的数量。例如,批量大小为 64 的一批图像(每个图像的形状为[256 × 128 × 3],其中 256 是高度(或行数),128 是宽度(或列数),3 是颜色通道数)的形状为[64 × 256 × 128 × 3]。在训练期间,一批数据样本与相应的目标标签一起通过模型进行预测(如果我们正在进行监督学习)。
epoch 是模型批量体验整个数据集的次数。单个历元包含一系列不同的多个批次(形成整个数据集),我们在训练样本批次的过程中对其进行迭代。对于随机学习,我们通常在每个历元迭代期间洗牌。
输出
让我们来分解清单 4-2 中发生的这么多事情。首先,我们在常量中加载批量为 64 个样本的数据集。然后我们宣布中的纪元数量为 2。
首先,我们有一个标记为的纪元循环。我们使用实例方法遍历的实例计算属性,该方法接受历元数(这里是,并在每个迭代步骤中依次返回一个数据点。在每一步,我们还用随机抽样的实例方法打乱批次顺序。
然后我们有一个标记为的批处理循环。我们遍历一个实例中的每个。在的主体中,我们从实例中提取和实例存储的属性。然后我们打印出这两者的以及和的迭代步骤。
我们在两个循环中都使用了方法来获取序列中迭代元素的索引。我们为循环定义了和标签,作为控制流语句的参考。你可以把和看作是循环的名字。如果我们简单地编写了语句,后面没有任何带标签的循环语句,那么 epoch 循环将执行两次,batch 循环将执行一次,也就是说,这将只停止 batch 循环执行多次。通过编写 ,我们告诉编译器简单地停止 epoch 循环本身的迭代,并执行其右花括号后的代码。
这里,我们加载 MNIST 数据集(LeCun,1998),它是从 0 到 9 的手写数字(每个图像一个)及其相应标签的灰度图像的集合。它们是由不同的人写的。正如我们在前面的清单中从看到的,每张图像的高度和宽度都是 28 像素,只有一个颜色通道使其成为灰度。这个数据集中的每个样本都是一个表示图像像素值(如)的和其对应的值(如)的元组。
机器学习算法的另一个重要部分是接下来讨论的模型定义。
我们可以很容易地定义模型架构,其属性可以在训练过程中进行区分。TensorFlow 中定义模型的方式主要有两种,一种是使结构符合特殊协议,另一种是使用受 Keras 启发的结构。
TensorFlow 提供了两种协议,即和,用于定义神经网络。可区分的模型定义结构必须符合这些协议中的任何一个。这些协议要求我们提供模型的和类型的实现为,定义方法,并声明至少一个 -或-符合或实例属性,其参数将在训练期间更新。
例如,让我们定义一个称为 LeNet 的卷积神经网络(LeCun 等人,1998)。
我们使用 Swift 的关键字定义了两个类型别名。这让我们可以在任何可以使用现有类型的地方使用现有类型的新名称。我们为类型定义了和类型名称。然后我们定义多个符合协议的神经层,例如、和。这里,是一个密集连接层(在 5.3.1 小节中解释过),是一个卷积层(在 6.1 节中解释过),层只是对层(这里)的输出张量进行整形,使其成为秩为 2 的批量向量。然后我们定义可微分的方法,它接受类型的输入并返回一个类型的值。在主体内部,我们在实例上使用实例方法。是在协议上定义的协议方法,因此可以被任何符合它的类型访问。它接受逗号分隔的符合的实例,并通过它们顺序处理。也就是说,在这里,首先由实例处理,其输出然后由处理,然后其输出最终由处理,后者再次返回类型为的新输出。这个输出然后由这个函数返回。注意,如果函数体、闭包、计算属性或返回某个值的下标中只有一个语句,我们可以去掉关键字。
接下来,我们解释这里使用的结构。
我们可以用 TensorFlow 中定义为结构的轻松定义一个多层神经网络。你可能会从 Keras 的设计中发现它的相似之处。
我们已经使用定义了清单 4-3 中的和。这样,我们可以简单地将多个神经层传递到 Sequential,每个神经层在不同的行中,后跟左花括号。我们甚至不需要像在协议一致性中那样定义实例方法。对实例的输入从第一层(最靠近左花括号)到最后一层(最靠近右花括号)依次处理。如 5.3.1 小节所述,神经网络中的小序列层被称为神经块,例如,和就是我们所说的神经块的典型例子。
加载数据集并定义模型后,现在让我们看看如何在数据集上训练模型。
在本节中,我们首先介绍 TensorFlow 中模型可微分参数的检查点。我们还使用定制的训练循环在 CIFAR-10 数据集上训练我们的 LeNet 模型。然后,我们再次用 Keras 风格的训练方法训练我们的模型。
训练神经网络是一项耗费精力和时间的任务。根据数据集和神经网络的大小,模型训练可以从几分钟到甚至几个月不等!训练找到模型的一组新参数值,对于该组新参数值,数据集具有非常低的损失值和高精度(在分类的情况下)。我们不希望我们花在训练模型上的时间被浪费。所以我们可以把最优的参数值写在磁盘上保存训练进度。这被称为检查点。当我们需要使用训练好的模型进行推理(例如,图像分类)时,我们可以简单地将参数从磁盘读入模型,并通过训练好的模型传递要分类的图像。
TensorFlow 允许我们创建模型的检查点。我们只需要使我们的模型结构符合协议。我们不需要写任何东西,只需要在后面加上左花括号和右花括号(见清单 4-4 ),所有在模型实例上可调用的方法都可以用于检查点目的。这之所以成为可能,是因为在协议中实现了检查点方法。
我们只是用扩展使符合!让我们声明一个目录的路径,我们希望在这个目录中读写检查点。这是通过从基础模块中定义实例来完成的,如清单 4-5 所示。
我们将设置为,以确保这个位置指向目录而不是任何文件。和都可能抛出错误,所以我们将使用一个 块进行错误处理,并用关键字调用这些方法。我们将在下面训练模型时直接演示这一点,而不是在这里演示。
让我们用随机梯度下降来训练我们的 LeNet 并节省检查点。清单 4-6 演示了培训。
首先,我们声明一个默认的 XLA 设备,所有的处理都将在这个设备上进行。我们将 CIFAR-10 数据集加载到常量中,并将其放在上。然后我们在变量中初始化我们的,并将其复制到。最后,我们为初始化 SGD 优化器(也复制到),使的和的(在 5.6.2 小节中解释)。
在清单 4-7 中,我们定义了一个函数,它接受和它们的作为参数。它为传递给的计算,然后与一起用于计算 softmax 交叉熵损失。函数将作为参数标签的一个参数,并接受一个闭包,该闭包计算并返回和之间的损失,这个过程在前一行中描述过。然后计算相对于所有参数的标量损耗梯度。最后,沿着其梯度??θ 的方向更新的可微参数。这结束了一个训练步骤。
输出
在清单 4-8 中,我们定义了一个名为的训练循环函数,它将历元数作为参数(默认为 5)。我们已经解释了数据采样(见 4.2 节)。对于每个,我们通过将采样的和传递给函数来执行单个训练步骤。在每个之后,我们在验证数据集上打印与模型准确性相关的统计数据,并且我们还将训练好的模型的参数写入到目录中,其中是模型的类型,即 LeNet。因为检查点写入和读取方法都可能抛出错误,所以我们在一个 块中使用了语句。
在清单 4-9 中,我们声明了一个唯一可获取的计算属性,它计算集合上的精度。我们将验证集中的样本总数设置为 10000,并从零个分类开始。遍历集合中的所有批次,我们生成,并将其与每个对应的进行比较,如果与匹配,则有条件地将变量加 1。请注意,我们在 softmax 激活的 logits 上使用方法来获取包含具有最高值的元素的向量的索引(请记住第一章中的内容,一个独热编码向量中的每个索引都属于某个类)。最后,我们返回正确分类的分数。
对模型进行训练后,我们得到 LeNet 在 CIFAR-10 上的训练精度等于 0.6187。
您可能已经注意到,定义训练步骤和循环、准确性属性以及其他内容会使程序变得稍微复杂一些。我们可以使用 swift-models 包中的 TrainingLoop 库来使我们的程序变得更小。它的灵感也来自 Keras 训练设计。训练循环目前集中在分类任务上。
让我们从头开始复制前面的程序,看看 TrainingLoop 是如何运行的。
在清单 4-10 中,我们导入了数据集、TensorFlow 和 TrainingLoop。然后我们声明一些配置,比如将设置为,将设置为。数据集、模型(使用清单 4-9 中的结构)和被初始化,如清单 4-9 所示。
然后我们声明类的实例,它跟踪与训练和测试相关的统计数据,比如损失和准确性。我们定义的下一个变量是,它将训练集和验证集、优化器、损失函数(这里是)和回调作为参数。然后我们调用上的方法,将模型作为参数、和进行传递,我们希望对其进行训练。这将执行训练过程并实时打印统计数据,而无需编写复杂的函数。训练完成后,该模型在训练集和验证集上的精度分别为 0.5607 和 0.5625。
注意,当使用 TrainingLoop 进行训练时,我们不需要将和复制到;方法为我们处理这一切。另一个需要注意的重要事情是,参数在循环的各种事件的训练过程中执行一系列函数。这里,我们只传递了统计跟踪函数,但是我们将看到如何通过定义我们自己的回调函数来保存检查点!
在本节中,我们实现了密集层、swish 激活函数、 L 、 1 损失函数和随机梯度下降优化器。这些例子演示了当某些东西还不能开箱即用时,如何实现自己的层、激活函数、损失函数和优化器,以用于研究或生产目的。这些例子也鼓励使用各种协议。我们鼓励您阅读 TensorFlow 的 API 文档 1 和代码库 2 、 3 、 4 ,以更深入地理解这些和许多其他协议。
定义新的神经层类似于我们定义自己的神经网络。我们不使用,而是让结构符合或协议。尽管协议可以实现与我们在 5.2 节构建线性模型时看到的相同的行为。现在,让我们通过使我们的结构符合协议来定义密集层(见 5.3.1 小节)。
是一个泛型,其类型占位符符合,本身符合。然后我们定义了的两个类型别名,即和,在可微分的实例方法中我们用它们作为我们稠密层的输入和输出类型。还有两个类型的存储属性,即和,是该层的参数。的初始化程序接受层的输入和输出特征的数量。该信息随后用于初始化和参数属性。最后,在正向传递期间,接受输入,对其执行仿射变换(即,和与函数矩阵相乘,并加上),并返回输出。
在对输入进行仿射变换之后,我们应用激活函数。许多激活函数分别变换张量的每个元素。图 4-2 所示的 swish 函数(Ramachandran 等人,2017)是激活函数的一个很好的例子。它由以下等式给出:

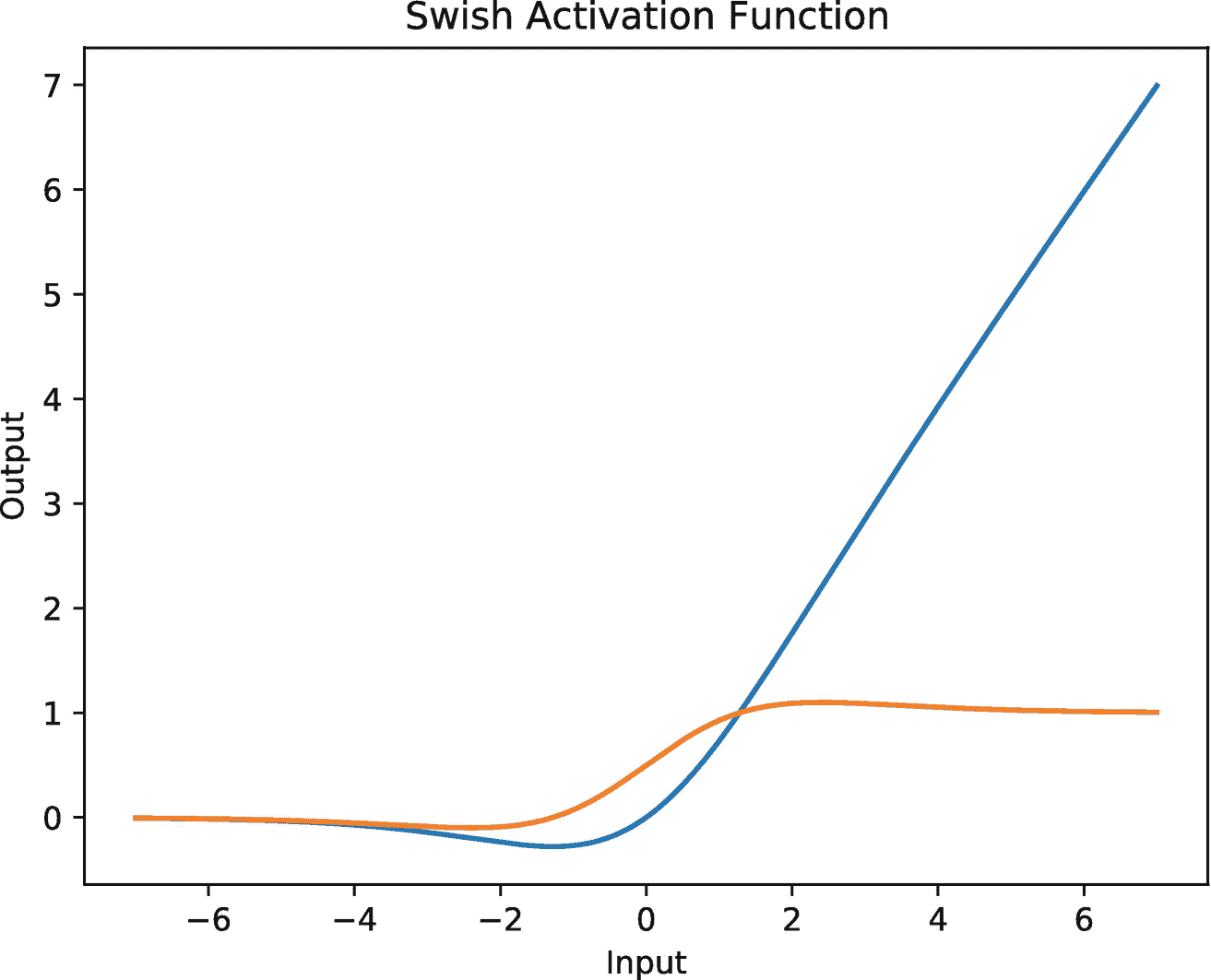
图 4-2
β = 1 及其导数(橙色)的 swish 激活函数图(蓝色)
这里, β 是一个可学习的或常数项。这一项通常设置为等于 1。因此 swish 函数变成如下:
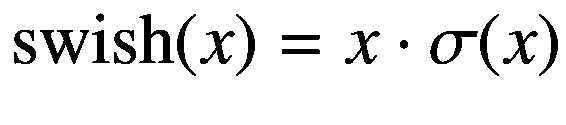
清单 4-12 演示了如何声明自己的激活函数(这里是 swish 激活函数)。
因为我们希望激活函数是可微分的,所以我们用属性来标记它。我们声明一个符合的泛型类型。这个函数接受参数并返回类型的输出。在的主体中,我们将与经过 sigmoid 函数转换的按元素相乘,并返回输出。我们可以在任何神经层的输出之后使用这个激活函数。
模型参数的值更新的方向由神经网络的预测(也称为 logits)和关于每个参数的相应目标(也称为标签)之间的损失梯度来引导。
在这里,我们描述如何在 TensorFlow 中实现自己的损失函数。我们展示了由以下等式给出的 L 1 损耗的简单实现。L1loss 计算逻辑和标签的每个元素之间的平均绝对误差(MAE ):
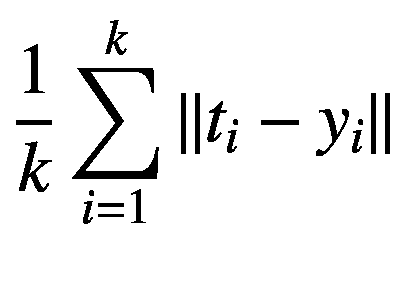
这里, y i 和 t i 分别是第 i 个索引逻辑和目标, k 是这些向量中每一个的元素个数。运算符∨。∑计算绝对值,即将向量的任何值的负号转换为正号。清单 4-13 展示了L1 损失的实现。
这里,函数将和作为输入参数,并返回一个类型为的值,其中是一个符合的类型占位符。这个闭包的主体计算和的对应元素之间的差,然后取其绝对值,并找到它们的平均值。
在训练期间,我们计算关于模型的每个参数的损失梯度,这给了我们最陡上升的方向。我们的目标是最小化损失函数,损失函数简单地由模型的预测和目标组成,因此我们在梯度的负方向上在参数空间中采取小的步骤。这被称为基于梯度的优化,在 5.1 节中讨论。接下来,我们看看如何在 TensorFlow 中定义我们自己的优化器。
我们可以通过使新的优化器符合协议来定义新的优化器。清单 4-14 通过重新定义随机梯度下降(SGD)优化器证明了这一点。
优化器必须始终被定义为一个类。我们定义了符合协议的类。我们还定义了一个符合协议的通用类型。然后我们为定义一些条件符合。我们说的必须符合和,必须是。每个协议之间的&符号()将所有这些协议组成一个协议。虽然这实际上并没有创建任何新的协议,但是这个协议组合表现为一个单一的协议。通过这种方式,符合(用于向量运算等等)、(用于算术)和(用于能够通过实例上的迭代其属性)。然后我们还要求的的(顾名思义,基本上是向量空间中的标量值)是类型。
我们为这个名为的类声明一个实例属性,它是优化的学习率。我们声明一个初始化器,它将类型的和类型的作为参数。这里,传递只是为了找到的类型,而不是为了在优化器中使用它。这是预期的行为。讨论请参考 GitHub 问题。 5 然后,更新实例方法简单地在相对于模型参数的损失函数的梯度的负方向上更新。它以的 和为自变量。存储的梯度。参数反映传递给函数的实例的变化。模型上的实例方法在用将其缩放至较小值后,在梯度的负方向更新其参数。我们总是将实例传递给前缀为&符号的参数。
本章重点介绍了深度学习编程,并介绍了 S4TF 的 TensorFlow 库。我们从解释如何创建张量实例开始。接下来,我们看到了如何在 TensorFlow 中加载数据集。我们还学习了如何创建深度学习模型,并对其进行训练和测试。我们还创建了模型的检查点。最后,我们学习了如何在 TensorFlow 中出于研究目的从头开始创建层、激活和损失函数以及优化器。在下一章,我们将了解神经网络的基础知识。
我喜欢胡说八道;它唤醒了我的脑细胞。
—苏斯博士
本章涵盖了神经网络的基础知识,也就是深度学习。我们讨论如下各种基础主题:基于梯度的输入和函数参数优化(5.1 节)、线性模型(5.2 节)、深度和密集神经网络(5.3 节)、激活函数(5.4 节)、损失函数(5.5 节)、优化(5.6 节)和正则化(5.7 节)技术。最后,我们在第 5.8 节总结了这一章。
在这一节中,我们介绍最大值、最小值和鞍点的概念。接下来,我们介绍输入和参数优化。输入优化将用于寻找函数的最大值和最小值。另一方面,参数优化将用于使用可用的函数映射数据集来查找函数本身。这两种优化在深度学习中都扮演着重要的角色,并将贯穿全书。在这里,我们主要关注在线的基于梯度的学习策略。在第 5.6 节中介绍了用于大型深度学习模型的更有效的梯度下降方法。
我们限制自己研究无约束最优化方法,因为它简单,并且满足我们演示书中提出的深度学习方法的要求。对约束优化感兴趣的读者可以参考(Deisenroth et al .,2020)教材的第 7 章。
这里,我们考虑一个标量函数 f : ? → ?.函数在某一点的导数有三种可能的值:正、负或零。在第一种情况下,当导数在某一点为正时,则函数随着输入的增加而增加。在第二种情况下,当导数在某一点为负时,函数的输出随着输入的增加而减少。换句话说,当输入少量增加时,导数的符号给出了函数增加的方向,可以是负的,也可以是正的。在第三种情况下,当输出不随输入的变化而变化时,那么导数在该点为零。
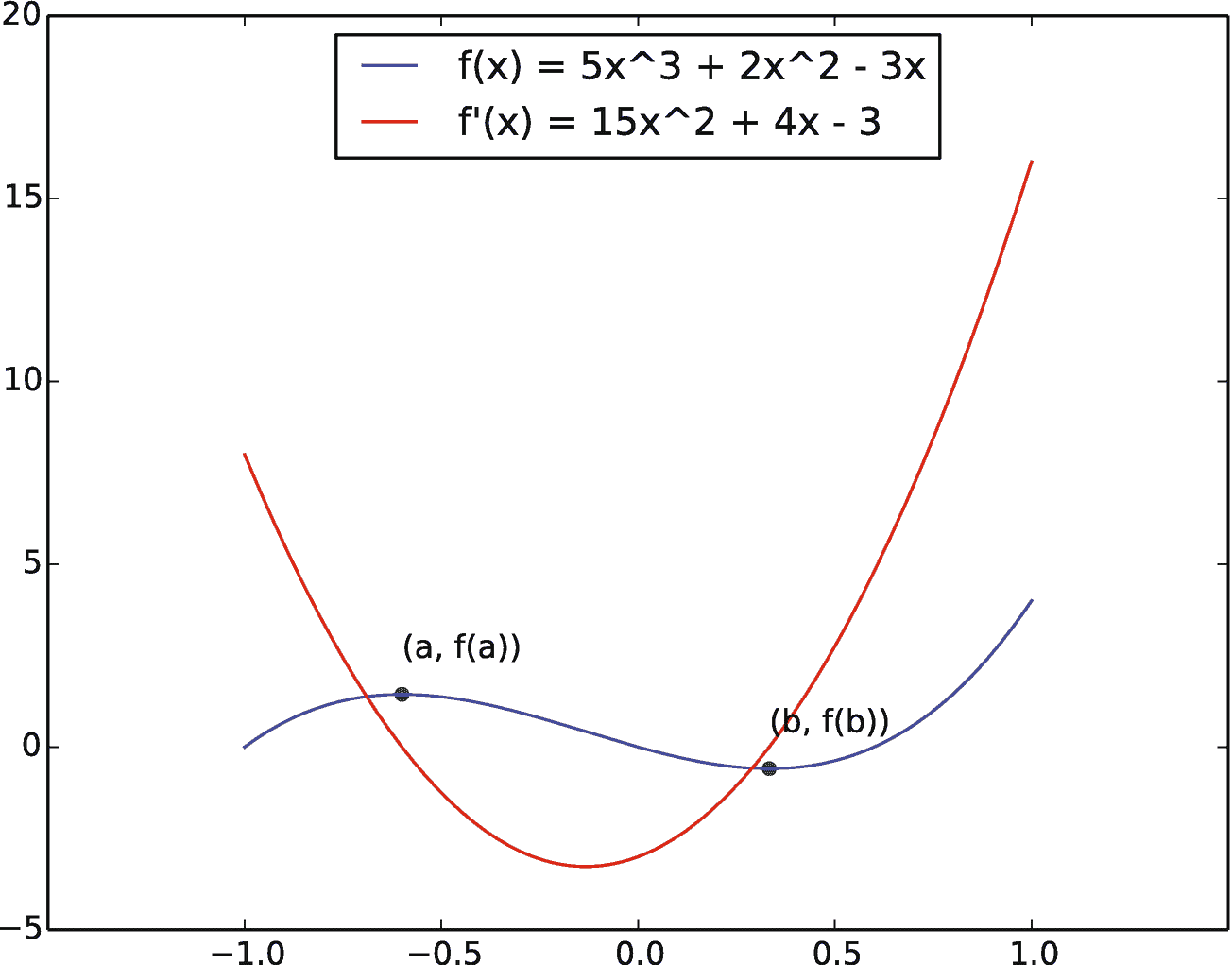
图 5-1
方程f(x)= 5x3+2x23x描述的函数有一个最大值和一个最小值。函数上一点的正切给出了梯度的斜率
图 5-1 为蓝色函数f(x)= 5x3+2x23x及其衍生函数f'(x)= 15x2 f 上的绿点( a ,f(a)=(3/5,1.44)和( b ,f(b)=(1/3,0.59)。)(蓝线)分别是函数的最大值和最小值。在这些点上,导数为零,即f'(a)= 0,f'(b)= 0。在水平轴上,从x= 1 开始,函数增加但缓慢减少,直到达到 x = a 。如前所述,这可以通过相同输入范围 x 中的相应红色导数线来验证;导数首先很大,但慢慢减小,直到在点 x = a 处变为零。这是函数 f ()变成零。函数上一点的正切给出了梯度的斜率。
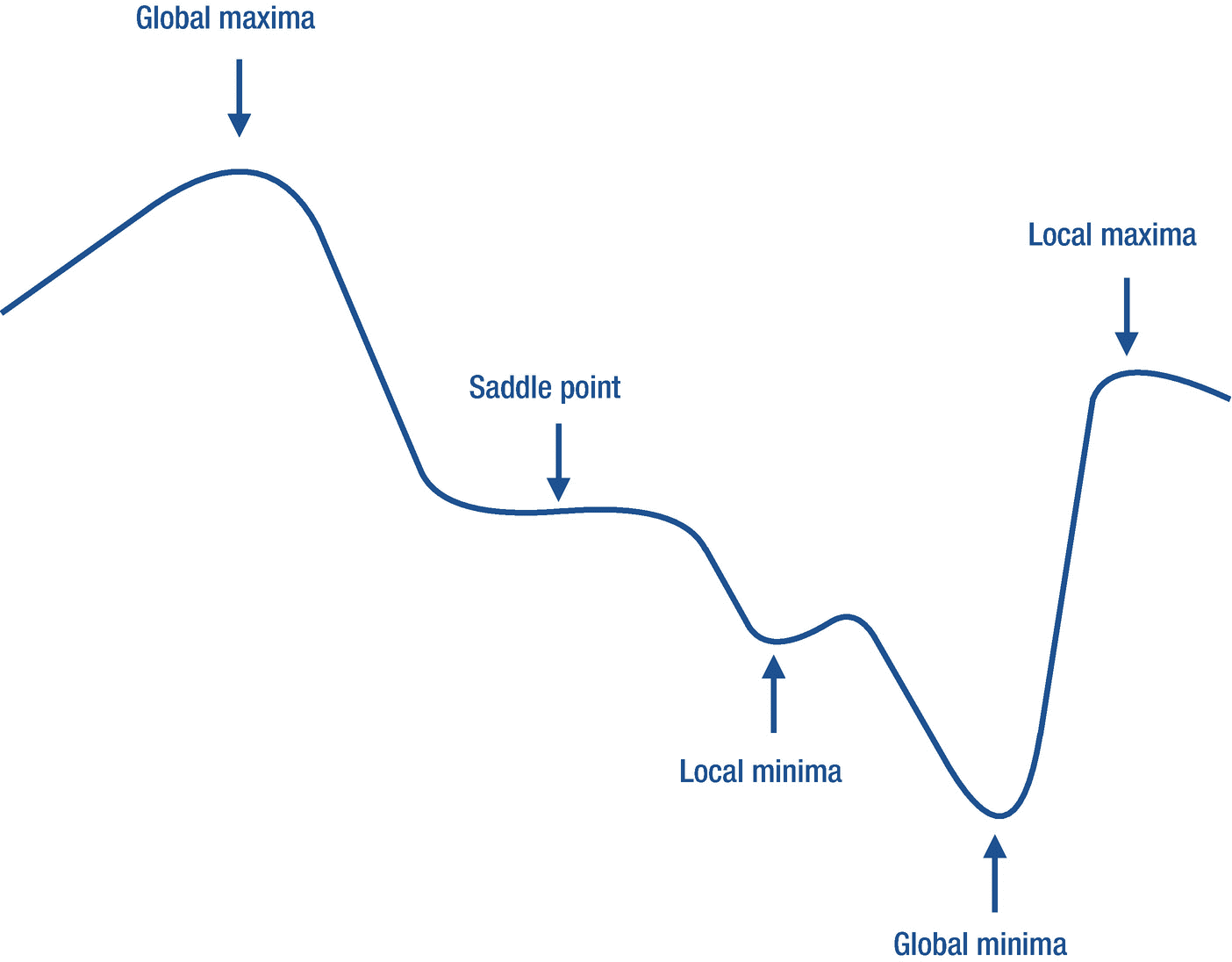
图 5-2
任意标量函数的最大值、最小值和鞍点的可视化
同理,从 x = a 到 x = b 开始,函数递减半个距离;然后对于另一半,它的变化率增加(但仍然是负的),使得它的斜率开始接近零,导数值也是如此。
函数 f (。)在 f ( a 处具有最大值,因为该函数在 x = a 前后的输出小于点 a 处的输出。形式上, f ( a ?)小于f(x=a)其中 ? 是一个小正数。另一方面,函数的最小值位于 x = b ,即 f ( b )的值最小。因为 f ( b ?)的值大于 f ( b ),所以函数 f (。)在 b 处有最小值。在最后一种情况下,当在一定的输入范围内时,输出 f ( x )保持不变,然后在这些输入值处的导数保持为零,满足条件f'(x?)= 0。该范围内的所有点称为鞍点。简单来说,在最大值,最小值,鞍点 x ,函数 f 的导数(。)始终为零,即f'(x)= 0。
最大值、最小值和鞍点的概念(见图 5-2 )不仅仅限于一元函数,也同样适用于高维函数,尽管很难在平面上可视化(如一张纸)。
在高中,通常遇到的数学问题如下:找出给定固定函数输出最小值和最大值的输入值。这些值分别被称为函数的最小值和最大值,如前所述。我们还知道,函数输出对输入的导数描述了输入增加时输出的变化率。
我们可以利用导数的方向信息,在数值上找到固定函数的最大值或最小值。例如,可以通过在输出相对于输入的导数的负方向上以小步长迭代地更新(或优化)输入值来找到函数的最小值(因为导数给出了函数增加最多的方向)。我们可以把基于梯度的最优化(柯西,1847)方程写成:
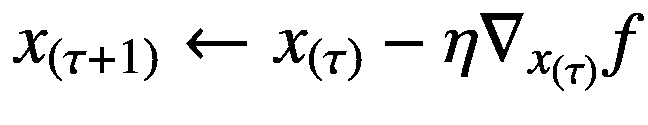
(5.1)
我们已经在方程 1.8 中遇到了一个更新函数参数的类似方程。这里,我们在多个步骤中迭代更新函数 f 的输入变量 x 的值。在这个等式中, η 是一个在范围(0,1)内的小正数,称为步长(或学习速率,在深度学习文献中, τ 表示时间步长,使得x(τ+1)是 x 在时间步长( τ + 1)的值
另一方面,有时我们可能需要找到一个函数的最大值。在这种情况下,我们可以简单地以小的步长在与导数相同的方向上移动输入,由下面的等式描述:
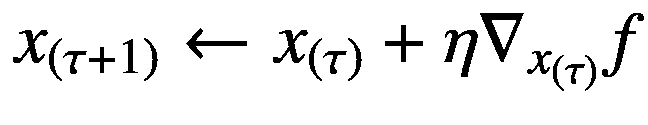
(5.2)
在基于梯度的优化中, η 项起着非常重要的作用。我们希望找到遵循输入更新的平滑轨迹的最佳输入值。因为导数在某一点上通常有一个大值,所以更新可能遵循一个不规则的轨迹,在最佳值附近表现出有弹性的行为。为了缓解这个问题,我们用 η 项缩小了导数值,这有助于按照平滑的更新轨迹更新值。
在清单 5-1 中,我们将最大化函数f(x)= 5x3+2x23x。
输出
我们先定义前面的函数f(x)= 5x3+2x2—3x。我们通过用属性标记它来使它可区分。然后类型的输入变量的初始值被设置为 0,步长被定义为设置为 0.01 的常数。我们可以看到优化前函数的输入输出值为零。
After gradient ascent, input: -0.5999994 and output: 1.4399999
// Optimization loop
for _ in 1...maxIterations {
/// Derivative of w.r.t. .
let ??xF = gradient(at: x) { x in f(x) }
// Optimization step: update to minimize .
x.move(along: ??xF.scaled(by: -η))
}
print("After gradient descent, ", terminator: "")
print("input: (x) and output: (f(x))")
Listing 5-3Find the minima of the function f(x) = 5x3 + 2x2 ? 3x
After gradient descent, input: 0.33333316 and output: -0.5925926
我们用属性标记。类似于等式 5.5 ,我们将目标和预测之间的差提高到 2 的幂,然后减半。
让我们在清单 5-5 中定义我们的数据生成函数。
我们将模型函数声明为一个存储了可微分属性的结构,如清单 5-6 所示。
当我们对这个损失函数的输出 e (称为误差)对预测输出进行偏导数时,我们得到一个简单的偏导数如下:
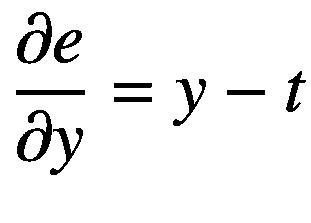
(5.6)
如果我们的模型是一个深度神经网络,那么这个误差通过关于先前变量的微分链规则进一步反向传播,然后在链的更深处传播,等等。在 Swift 中,这是通过使用一种称为算法微分的更通用的偏导数计算技术来完成的(参见第 3.3 节)。
在通过损失函数进行参数优化的更有意义的问题公式化之后,参数更新方程 5.3 现在变成如下:
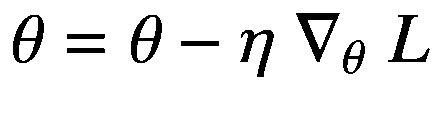
(5.7)
这里, L 是损失函数;并且类似于方程 5.3 ,我们更新方程 5.7 中的参数 θ 。让我们看看清单 5-7 中的参数优化。
Before optimization
▽ ParametersOptimization.Function
- a: 1.0
- b: 1.0
- c: 1.0
After optimization
▽ ParametersOptimization.Function - a: 4.9880642
- b: 2.0008333
- c: -2.9924128
我们已经声明了一个由权重项和偏差项组成的线性模型结构。接下来,我们将模型与来自数据生成函数 g 的样本进行拟合。).
Before optimization
▽ LinearRegression.LinearModel
- w: 1.0
- b: 1.0
After optimization
▽ LinearRegression.LinearModel - w: 4.9880642
- b: 2.0008333
struct PolynomialModel: Differentiable {
var weights: [Float]
var bias: Float = 1
@noDerivative var order: Int
init(order: Int) {
weights = Array(repeating: 1, count: order)
self.order = order
}
@differentiable
func callAsFunction(input: Float) -> Float {
var output = bias
for index in 0..<order {
output += weights[index] * pow(x, Float(index))
}
return output
}
}
Listing 5-10Declare a polynomial model
接下来要做的事情是声明一些配置常数,例如网络的图像样本通道、CIFAR-10 数据集中的类的数量、训练模型的时期数量、样本的小批量大小,以及一些类型别名,以便于初始化将在其上执行每个训练相关操作的设备。
网络接受的输入通道有三个,CIFAR-10 数据集的图像大小为? 32×32×3 维,网络可以预测的类别数设置为 10,网络将经历数据集 50 次,每个样本为一批 128 幅图像,批维数为? 128×32×32×3 。我们将设置为 XLA 后端,默认设备将被自动选择,也就是说,如果选择了一个硬件加速器(如下所述),则为 CPU。
如果你在 Google Colaboratory 上编程,你可以选择硬件加速器为 GPU 或 TPU,方法是在菜单栏中点击运行时?更改运行时类型,然后从弹出菜单中的硬件加速器下拉列表中选择任一设备,并点击保存按钮。现在将自动设置为 GPU 或 TPU 加速器与 XLA 后端,将在选定的加速器上训练。在我的实验中,我选择了 GPU。

图 6-8
残差卷积块的详细架构
输入经过卷积和批量标准化层、ReLU 激活以及另一系列卷积和批量标准化层。该输出与剩余输入相加,然后用 ReLU 激活剩余输入,给出剩余模块的最终输出。残差输入首先被投影(或下采样)到与第二批归一化层的输出相同的维度(即,输入的一半)和通道(即,输入的两倍),但是如果通道和维度相同,则它被原样传递到残差连接。
现在我们将对清单 6-3 中的块进行编程。
让我们从名为的实例的初始化开始,它以、和作为参数。第一个自变量是四个值的元组,其中第一、第二、第三和第四值分别代表内核的高度、内核的宽度、内核的深度(即,输入特征图的过滤器)和内核的数量(即,输出特征图的过滤器的期望数量或深度维度大小)。第二个自变量是两个值的元组,其在第一和第二索引处分别表示在应用卷积运算之前在高度(即,垂直)和宽度(即,水平)方向上采取的步骤。第三个参数是我们已经讨论过的枚举类型的。在 TensorFlow 中,我们不需要计算零填充并将其放在卷积或池化等层中。我们可以将设置为或。两者的区别在于在输入周围应用零填充(如果需要)以产生与输入相同的空间或时间维度的输出,而在输入周围不应用任何零填充,并且输出的空间或时间维度可能与输入的空间或时间维度相同,也可能不同。但是在我们的代码示例中,我们将主要使用枚举的用例。最后,我们没有在我们的实例中使用偏差项,并将参数设置为等于。
接下来,注意批量标准化层采用的参数等于卷积层的输出滤波器数量。我们还将的和分别设为等于和。
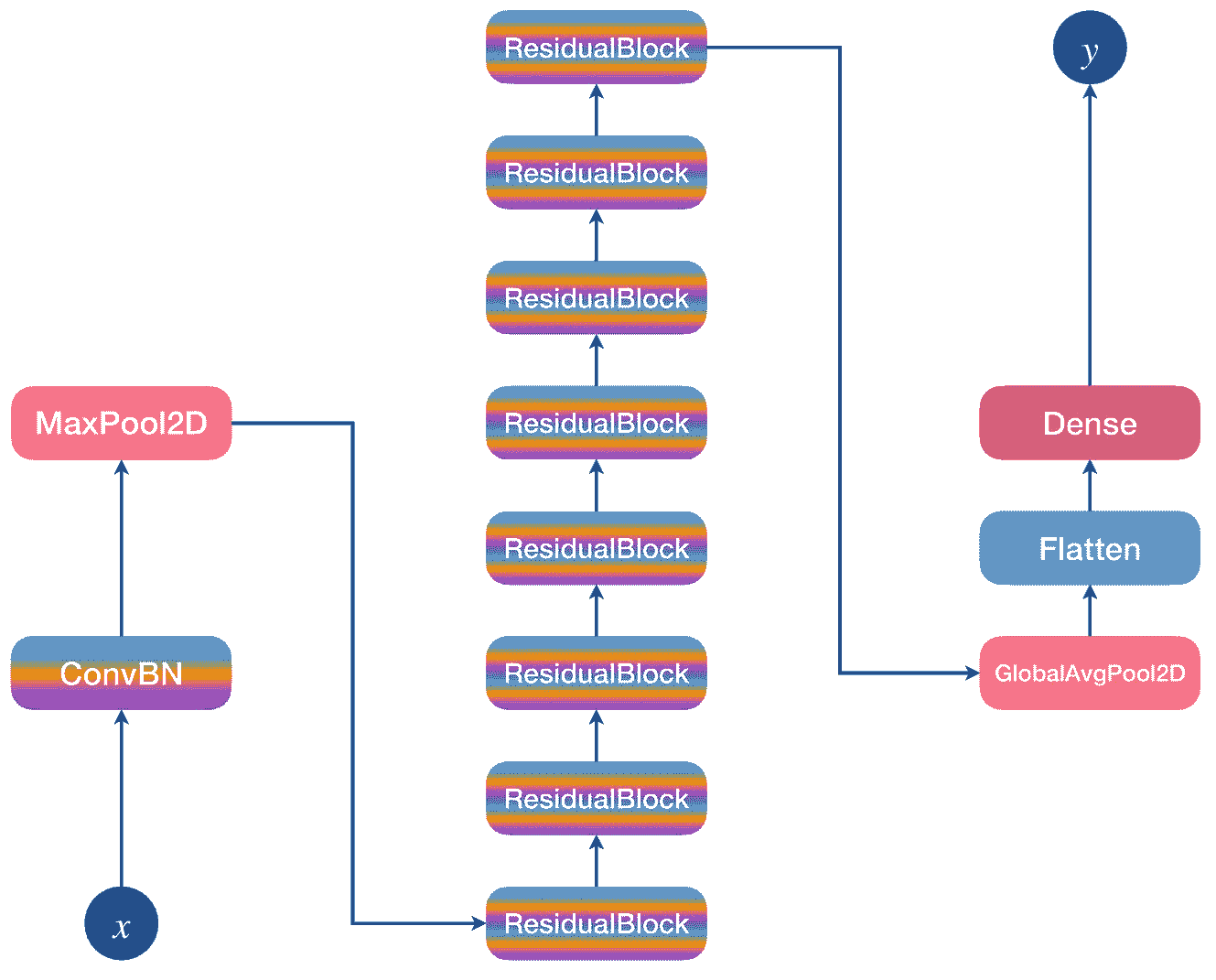
图 6-9
18 层剩余卷积网络的详细结构
输入x∈?b×224×224×3经过卷积和批量归一化层和 ReLU 激活,随后是最大池操作。这里, b 是最小批量。然后,输出经过一系列八个残差块,其输出经过全局平均池操作、展平层(将多维张量转换为批量向量)和密集层,后者产生罗吉斯向量 y ∈ ? b×10 。
现在我们将对清单 6-4 中的剩余程序块进行编程,如图 6-8 所示。
残差块是 ResNet 模型的基本构造块。残余块的可视化和解释见图 6-8 。在清单 6-4 中,名为的残差块结构有三个存储属性,即、和类型的。在其初始化器中,它接受前两个参数,即和。初始化层时,我们检查和是否相等。如果这是真的,那么我们为和设置内核的高度和宽度等于 3 个单位。和的输入通道设置为等于和,两者的输出通道设置为等于。
两层的也默认为。在这种情况下,由于默认情况下为而为,输入输出特征尺寸将相同;因此,我们不需要投影输入,我们将实例初始化为默认值。
当的和不同时,我们将的设置为等于,而对于和的其他参数与前一种情况相同。使用此值,输入要素的空间维度将减半。因此,我们将实例的所有参数设置为与相同,以将输入投射到与和序列将投射的维度相同的维度。
在方法的正向传递过程中,如果两个序列的输入和输出滤波器不相同,但在其他情况下等于输入本身,我们首先将剩余输入设置为等于投影输入。然后我们应用并用激活它,运行通过,加上剩余输入,用激活它返回剩余块的输出。
清单 6-5 显示了 ResNet18 模型结构。ResNet18 模型如图 6-9 所示。
如图 6-9 所示,该结构有四个块,每个块包含两个,还有和属性,执行卷积和批量归一化以及一个最大池操作。有一个名为的平均池属性和一个类型为的属性。最后,我们有一个类型的属性用于预测。在正向传递中,输入张量通过、、、、、和传递。输出是输入图像的卷积特征,然后汇集、展平(即整形为批量矢量),并通过层进行预测。
接下来,我们侵入协议,用 NumPy 数组实现读和写检查点方法。
我们在协议上声明了两个实例方法,所有符合它的类型都可以自动使用它们,即和。检查点写方法声明了一个类型的参数数组。然后我们通过可以写入的遍历类型的所有属性。在通过调用方法将实例转换为 NumPy 数组之后,我们将每个属性添加到数组中。在循环之后,我们将 NumPy 数组类型转换参数保存到文件位置。
在检查点读取方法中,我们加载检查点文件。然后,我们递归地迭代指向类型的所有可写的,并通过强制展开将处的符合层的实例的属性设置为等于从索引处的加载的 NumPy 个参数。这样,我们将参数加载到我们的一致性实例中。
接下来,我们定义一个函数来保存训练期间每个时期结束后的检查点。我们将把它传递给数组中的参数。在训练过程中,接受一组基于特定事件调用的函数。
在清单 6-7 中,我们定义了一个占位符类型符合的函数,它带有两个参数:类型的和类型的。这个函数会抛出一个错误。如果您想在训练期间通过传递给为其他定制任务定义您的函数,您应该使用相同的参数,并在函数体内定义定制功能。
在主体内部,我们有一个包含在中的语句,用于使用另一个线程来执行这个任务(您可能不需要编写这个语句,但是我在代码执行方面遇到了一些问题)。语句将事件参数与各种情况进行比较。因为我们想在每个时期结束时保存检查点,所以我们试图在等于的时候写检查点。还有许多其他的案例,你可以利用它们来定制训练循环。
在清单 6-8 中,我们已经用具有类的初始化了用于预测。优化器用随机梯度下降优化器初始化,该优化器具有学习速率和等于的动量设置。然后分别初始化和实例和。对于和,用初始化,优化器被设置为等于,损失函数被设置为,是包含更新方法和函数的数组。
最后,我们对进行训练,在训练集和验证集上分别达到 0.9960 和 0.7305 的图像分类精度。我们的 ResNet18 模型的性能优于在相同数据集上训练的小 LeNet(参见第四章),后者在训练集和验证集上的精度分别仅为 0.5607 和 0.5625。
在这一章中,我们研究了卷积神经网络对于处理计算机视觉问题非常有用,并且比密集网络有许多优势。我们还研究了一种减轻梯度消失问题的技术。最后,我们训练了一个深度卷积网络来对图像进行分类,其性能优于一个较小的卷积网络,表明深度非线性模型优于浅层模型。
这本书用 Swift 为 TensorFlow 介绍了深度学习学科。但我们只是触及了深度学习领域的皮毛,还有很多东西需要了解!我希望你喜欢用 Swift 语言理解和编程深度学习。直到下一次…
以上就是本篇文章【Swift-和-TensorFlow-深度学习教程-全-】的全部内容了,欢迎阅览 ! 文章地址:http://www.riyuangf.com/quote/16529.html 行业 资讯 企业新闻 行情 企业黄页 同类资讯 网站地图 返回首页 迅易阁资讯移动站 http://qyn41e.riyuangf.com/ , 查看更多